• Information for Parents
• Information for Students
• Information for Educators

UPDATE, July 28, 2014: IMACS has completed the update of our AP^® Computer Science: Java Programming course to include eight fully-elaborated labs that far exceed the minimum requirements of the College Board. IMACS’ Be Prepared for the AP^® Computer Science Exam online course has been updated as well. Students who are enrolled directly through eIMACS in our AP^® Computer Science: Java Programming online course receive free access to the Be Prepared course.

Following a recent review of the AP^® Computer Science A course and exam, the College Board has decided to replace its case study requirement with a requirement to complete a minimum of 20 hours of hands-on lab experiences. This change, which will take effect for the 2014-2015 school year, is being implemented to more effectively support student learning of core concepts in computer science. IMACS continues to follow closely all communications from the College Board, as well as discussions within the APCS community, on the forthcoming changes and will act accordingly.

From the beginning, IMACS’s philosophy has been to emphasize computational thinking and mastery of foundational ideas in computer science. This approach is reflected in how our Curriculum Development Group has meticulously designed our CS courses and, more importantly, in the success our CS graduates find in college, graduate school and at top tech companies. As such, IMACS fully expects that our AP^® Computer Science: Java Programming course will continue to exceed, as it always has, all of the College Board’s requirements and remain College Board-approved.

GridWorld Case Study

Since the 2007-2008 school year, AP^® Computer Science A has used the GridWorld Case Study to reinforce lessons on object-oriented programming.* GridWorld provides Java code designed to simulate the behavior of objects (Rock, Flower, Bug and Critter) in a grid. Ground rules such as Rocks cannot move, Critters eat Flowers and Bugs move forward and turn 45 degrees if blocked are part of the initial set-up. Given these starting parameters, students then write additional code that extends these various classes of objects. A student’s understanding of computer science concepts in the context of the GridWorld code is then tested on the AP exam with one free-response question and a handful of multiple choice questions.

College Curriculum Study

In 2011, the College Board undertook a College Curriculum Study in which institutions of higher education were surveyed about the AP^® Computer Science A course case study.^ Of the 117 institutions that responded, 91% said they were not likely to change their credit/placement policy for AP^® CS A if questions on the case study were not included in the exam. About two-thirds of respondents rated the inclusion of a case study as not important or only somewhat important.

Clearly, GridWorld is now past its prime. As the College Board noted on its website, the case study requirement in AP^® Computer Science A needed updating “to stay aligned with the most recent practices in the continually changing field of computer science.”

Labs, Labs, and More Labs

This March, the College Board plans to release details of three sample AP^® Computer Science A labs as examples of how the new lab experience requirement may be implemented. One expectation is that their shorter length will make the labs easier to integrate into the course curriculum throughout the school year. Teachers and curriculum developers will have the flexibility to include sample labs or other comparable labs at points they feel are most relevant and pedagogically effective. It is also expected that the sample labs will be more connected to real-world situations, perhaps increasing student interest in taking the course and studying computer science.

Most importantly, labs are expected to support student learning of fundamental ideas in computer science. Whereas the case study questions on the current exam are tied heavily to the context of the GridWorld code, the 2015 AP^® Computer Science A Exam will test a student’s understanding of core concepts that are reinforced by hands-on lab experience, not knowledge specific to any particular lab. As an educational institution that has always emphasized foundational concepts in CS over code manipulation skills in the programming language du jour, IMACS is pleased to see the College Board take this important step.

Learn how you can give your child an unfair advantage in computer science. To find an IMACS teaching center near you, visit www.imacs.org. Talented middle and high school students can take university-level computer science online through our eIMACS distance-learning division.

*For readers who may be unfamiliar with object-oriented programming, it’s an approach in which the programmer creates “objects” with specified attributes and behaviors as modular, reusable code.
^https://tinyurl.com/LabsAPAC2013

The following letter is extracted from the new book, Letters to a Young Math Teacher, by Gerald Rising and Ray Patenaude, which is available from Amazon.com and other sources. Gerry Rising is Distinguished Teaching Professor Emeritus at State University of New York at Buffalo where he co-founded the university’s Gifted Math Program for highly-qualified regional students in grades seven through twelve. Gerry Rising was for many years associated with IMACS activities and is a strong supporter of our work.

Paul Rosenbloom enjoyed an international reputation as a senior mathematician when I joined his Minnemath Project at the University of Minnesota as his assistant director. His Elements of Mathematical Logic remains today a basic resource recognized worldwide to be of historical as well as academic significance.

In our very first conversation he told me that he considered teaching outside the classroom an important aspect of a mathematician’s life and he urged me to develop what he called “a bag of tricks” from which to draw math-related lessons for people of all ages. I would later see him draw from his own collection in a number of settings. He could captivate anyone from nursery school students to scientific colleagues and even senior political figures.

Within a month of that conversation I found myself seated on an airplane flying from Minneapolis to Denver. My seat partners were a bored nine-year-old and her mother. When the mother learned that I was a math teacher, she asked me if I would be willing to “show Marjorie some math.”

Fortunately, I had been reading David Silverman’s book, Your Move, and I had some pennies with me. I played a series of Nim games with Marjorie, finding her an interested opponent and a remarkably quick study.

Nim, for readers unfamiliar with the word, is German for “take” and in this context it applies to games with players taking one or more counters like coins from a collection following a given set of rules.

We started with One Pile Nim. I set out a line of pennies on Marjorie’s tray and explained the rules. We would take turns, at each turn removing one, two or three coins. The winner would be the player who could take the last penny or pennies.* When she quickly determined the strategy for playing, I suggested she challenge her mother. Her eyes lit up as she outplayed her mom.

Now she wanted more. I suggested the misère form of the game: same rules for play but this time the loser forced to take the last coin. Now I had her mother’s full attention as well, but again Marjorie, once she found the winning strategy, could outplay mom.

We went on to play the very simple Two Pile Nim game in which each player takes any number of coins from one of two piles with the winner taking the last coin, but then the less transparent game, Woolworth, which is isomorphic to Two Pile Nim. Woolworth is named for the five-and-ten-cent stores of the 1950s that have been reincarnated as today’s Dollar Stores. On a sheet of paper I drew the following diagram:

I placed nickels and dimes as shown in the figure. One player controls the coins on the left, the other the coins on the right. Players alternate moving either of their coins any number of squares to left or right but without joining or passing the opponent’s coins. The object of the game is to squeeze your opponent so that no moves remain.

By the time I showed Marjorie the connection between Two Pile Nim and Woolworth we were well on our descent into the Denver airport. I was rewarded for our hour together when Marjorie turned to her mother to tell her that she wanted to become a mathematician.

Where do you find lessons like these that require no background and yet are suitable to given age groups? I found mine from two sources: my reading of journals and books about mathematics and my observation of lessons taught by others. Appendix 2 lists a few of the many available book sources.

Now, because it is a good story, I will tell you about my use of a lesson copied from the remarkable teacher, Robert Wirtz.^

Late one school year when I was a math supervisor I was asked by a primary school teacher to demonstrate Stern blocks for her students. Stern blocks are inch cross-section blocks that come in lengths from one to ten inches. Cuisenaire rods are similar but with centimeter dimensions.

I took several sets of Stern blocks to this teacher’s classroom and showed the six-year-olds some of the relationships among them.

The students were excited by the opportunity to mix play with learning, and I was convinced that they were gaining from the lesson. I noticed, however, that their teacher was not happy with the children’s mix of play with learning. Several times she interrupted their activities to tell individuals to be quiet.

It was clear to me that the teacher was convinced that I wasn’t disciplining the children in the way she wished, so I suggested that I return the next day to teach another lesson. Despite her reservations about my conduct of this class, she jumped at the chance to have me return. It was clear that she was happy to pass responsibility for these irrepressible kids off onto anyone she could find.

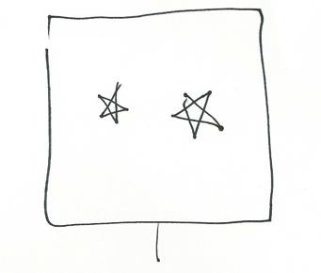
I had seen Bob teach a lesson to a similar group and the next day followed his model. Before the class I had the teacher gather the students in front of the chalkboard. Saying nothing to them I drew a square on the board and within it marked two star shapes. What I had drawn looked like this:

I pointed to that little tail at the bottom of the figure and turned to the class, holding out the chalk.

Several hands waved and I offered the chalk to one of the wavers. The boy came up and carefully wrote a “2” below the diagram.

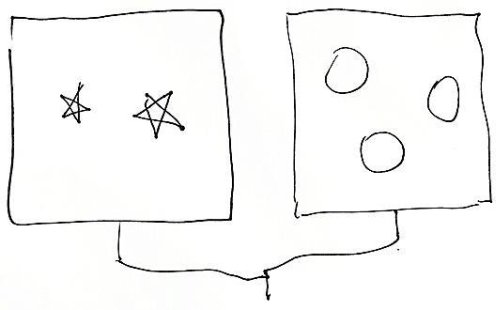
That got us started. I drew similar diagrams with different shapes and the children quickly caught on, competing to write the numbers below the figures. Then I began to complicate the requests by erasing their numbers and connecting two figures like this:

No problem. A volunteer wrote “5” below the boxes.

I continued in this fashion, soon replacing the boxes with numbers but using the same connecting segments. All of the children were eagerly participating, but not one word was said by me or by any of them.

After a half hour of this activity, I finally spoke up, calling the children’s attention to the fact that none of us had spoken until then. And I turned to their teacher to congratulate them on what we had accomplished.

Unfortunately, my lesson proved nothing to this young woman. Her response: “Yes, after you left yesterday I really scolded them for their behavior and you saw the result this morning.”

Even with the best of efforts, you cannot always win.

I have talked about these mathematical extras mostly in terms of their use outside of your classroom, but they can play a role in your classes as well. Here is an example described by Swedish math educator Barbro Grevholm:

Please take the examples I have used only as samples of my own and others’ collections of activities. You may or may not add them to your collection. What is important is that you accumulate such activities that work for you. They will serve you well.

Sources of such activities are all around you. You just have to be alert to them and adapt them creatively.

Many such activities come from your reading. Mathematics and mathematics education journals describe topics and lessons that you can both enjoy and share with others. Of course, you should credit your source when you replicate such a lesson, but every writer I know would be delighted to know that his or her lesson was being duplicated.

The two best journal sources I know for such examples are the Mathematical Association of America’s Math Horizons and the British Mathematical Gazette.

Some non-standard texts are full of such lessons. Authors like Harold Jacobs and Sherman Stein are two who have gathered and present such useful topics. And some authors simply collect such presentations. Among these are Ian Stewart, Ross Honsberger and Howard Eves.

In a class by himself is Martin Gardner whose collections of such topics are unsurpassed. His range is amazing, covering everything from hexaflexagons to fractal music, almost all of them serving a perfect basis for well-planned demonstrations.

Even your daily newspaper can provide activities. Although many people are drawn to the Sudoku puzzles, I much prefer three other popular forms: Kakuro, KenKen and Numbrix. These puzzels are adaptable to students of all ages (I solve one or two each day) and can challenge them all. The simplest appearing is Marilyn vos Savant’s Numbrix. While this puzzle task is appropriate for primary grade students (all it involves is listing the integers from 1 to 81 in order in a 9×9 grid), individual Numbrix puzzles range widely in difficulty.

In addition to their intellectual challenge, there are two things about the Kakuro and KenKen puzzles that I find attractive: (1) they involve basic calculation facts that reinforce the solver’s skills and (2) they appear as free apps on mobile phones and tablets. This availability makes them perfect puzzles to introduce to fellow travelers.

* The strategies for playing these Nim games are included in Appendix 4. I encourage you to play the games before you look at those strategies.

^ Bob Wirtz and his wife adopted a number of children with severe learning problems and they developed math materials to teach them. With Mark Botel, then president of the International Reading Association, he gathered those materials into books for elementary school students. Sadly, they are difficult to find today for they include some very attractive activities.