• Information for Parents
• Information for Students
• Information for Educators

The IMACS Blog reconnects with alumnus Mark Engelberg who recently released three new coding games through ThinkFun and Target. (Win an autographed copy of one of Mark's new games!) Mark's passion for computer science, math and logic led him to an award-winning career in puzzle and game design. He is also an active speaker in the Clojure programming language community. In this post, Mark talks with IMACS about what it was like to be a homeschool dad to two amazingly talented children who are now accomplished young adults in their own right.

First, tell us about your new ThinkFun games.

Two years ago, I invented a programming puzzle game for ThinkFun called Code Master. Code Master was a commercial and award-winning success, so ThinkFun asked me to develop a new line of puzzle games, where each game would highlight a specific underlying principle of computer science. The new line of games is called the //CODE Programming Game Series. To design the games, I started from a list of concepts I wanted players to encounter, and kept trying out ideas and tinkering with the rules until I felt I had a combination of mechanisms that covered those concepts and was fun to play.

The first game in the series, On the Brink, is an introduction to procedural abstraction — the idea that we're not just writing programs to solve a one-off task, we're building components that solve multiple instances of an underlying problem, and then using those components to build higher-level components, and so on. The second game, Rover Control, focuses on the essential skill of stepping through programs in your head and visualizing the outcome, particularly with flow control constructs like if-then-else statements, while loops and for loops. The third game, Robot Repair, is all about Boolean logic. When developing Robot Repair, I leaned heavily on the material that I learned as a child in IMACS' Advanced Mathematical Logic courses. I think students in your Logic courses are really going to enjoy Robot Repair. Like their predecessor, Code Master, all three of the new games are "unplugged" computer science board games that come with a book of puzzles for solo or cooperative gameplay.

You are also a parent of two gifted children who are now ages 19 and 17. About how old were Alex and Molly when you first suspected that they were gifted? What were the signs?

I was a stay-at-home dad, and when Alex and Molly were toddlers, I taught them to read and write and gave them daily math lessons. Honestly, I mostly did those things to keep myself from getting bored; it was fun for me to feed their intellectual curiosity. My wife did the same with the kids when she was home from work. That was just our parenting style. We wanted the kids to have the opportunity to learn these core skills as soon as they were capable, and the easiest way to achieve that was to throw a lot of educational activities at them early, just to see what would stick. As it turned out, more of it stuck than we expected!

I didn't really have much to compare their development to until the day I went to Alex's kindergarten orientation. As the teacher explained what the students would be doing in the coming year, it dawned on me that my kids had already done those things. I realized that I had inadvertently given my kids a big jumpstart, and what I had been doing was working, so I might as well keep doing it. And that's how I ended up deciding to homeschool my kids.

Because I homeschooled my kids, the label "gifted" didn't really come into play. I never needed to get them tested, or prove anything to a school official. But it was clear to me that they had the capacity to learn faster than what our school system provides, so I set out to do my best to keep them challenged and allow them to fully develop their individual talents.

How did you feel when you knew for certain that they were gifted?

It felt like a tremendous responsibility to help them achieve their full potential, even more so because I was choosing to take on that responsibility myself rather than relying on the school system. If things didn't work out, I would have no one to blame but myself. It was a lot of pressure. I didn't really doubt my capability to teach them, but I knew it would be an enormous undertaking, one that would require the bulk of my time and attention for nearly 20 years. It was well worth it — I'm so proud of the young adults they've become — but I'm relieved to have reached the point where that responsibility is behind me rather than in front of me.

As you looked into ways to meet their educational needs, what did you discover?

One pleasant surprise was realizing that it isn't necessary to be an expert in everything in order to meet your kids' educational needs. In many cases, it's more about playing the role of an advocate, connecting them up with the right resources. I would track down private teachers, public school classes, homeschool co-op classes, other parents, books, videos, and websites for the areas I was less equipped to handle. I did my part for the homeschooling community by serving as a teacher of math and computer science for many other talented kids whose parents were not as adept at those particular subjects.

What were some of the programs, opportunities or approaches that you found helpful in making the most of their talents and interests?

One of the things that was really important to me was to make sure my kids had a strong foundation in math and computer science. Fortunately, I have the advantage that I learned the IMACS curriculum when I was in middle school and high school. This made it easy for me to teach these subjects because I'd already experienced first-hand what a top-tier math and CS education looks like. To duplicate that experience for my kids, I simply taught them using the same materials and techniques that I had learned at IMACS and in college. Those resources played a big role in giving me the confidence to homeschool.

What were some of the benefits and challenges of homeschooling? How did you deal with the challenges?

One of the biggest challenges of homeschooling is that it takes effort to find a community to be a part of. We are fortunate that here, where we live in Seattle, there is a robust homeschooling community and we were able to find a group that fit our personalities and make many dear, lifelong friends. Once we found the right community for us, those rich social interactions became one of the biggest benefits of homeschooling. Our weekly park days remain some of my most cherished memories.

Another big challenge is that, even though my kids are close together in age, they were far enough apart that I couldn't do the same lessons with them. I always felt like I was struggling to give each of them the level of individual attention I wanted to give them. My solution was to make certain parts of the day relatively structured and leave the other parts of the day flexible so that I only needed to schedule the structured parts. For example, I might be doing structured math lessons with one child while the other was doing creative writing or watching an educational video, and then switch.

What were some other challenges you faced in parenting gifted children, and how did you deal with those?

Gifted children can be wildly asymmetric in their abilities, and wildly different from one another in terms of their talents and interests. It was a constant challenge to avoid getting impatient when one of my children would struggle with a concept that came naturally to the other. I had to keep reminding myself that it was totally normal for them to have different strengths and weaknesses.

How did being a gifted adult who was once a gifted child affect your educational and non-educational parenting choices?

This was especially helpful when my kids' interests dovetailed with my own. My son, for instance, developed a keen interest in programming, and thanks to my own background, I knew exactly what to do to support him in that interest. When my kids' interests and abilities diverged from mine, it was a lot tougher, and I ended up doing what any parent would do … seeking out people and resources that could help my kids develop their talents.

What are your fondest memories of raising Alex and Molly?

Probably my fondest memories are the many times we played board games together over the years. For those moments, instead of having a parent/child relationship, or a teacher/student relationship, we were just people playing games together and enjoying each other's company. I feel like at those moments, I really gained some insight into their character, and got a glimpse of what they would be like as adults.

What are your hopes for them in the future?

My hope has always been for them to be good, caring, compassionate, independent, happy adults. The good news is … they already are. I'm done! Woohoo!

Robot Repair Raffle

Robot Repair was inspired by Mark's study of the IMACS’ Advanced Mathematical Logic curriculum.

Residents of the continental United States are eligible for the Robot Repair Raffle. The autographed copy of Robot Repair will be shipped only to an address in the continental US. To enter the raffle, complete the following steps:

1. Parents must register their child to take either the EMF Aptitude Test (ages 10-14, approximately) or the eIMACS Aptitude Test (ages 14-18, approximately).
2. On the aptitude test online registration form, type "IMACS Blog" in the box for "How did you hear about us?" or "How did you hear about IMACS?".
3. Have your child take the aptitude test for which he or she is registered. The test must be taken during the period October 1-30, 2017. (No minimum test score is required to qualify for the raffle.)

The IMACS Blog has recommended several games, puzzles, and apps that encourage structured mathematical or computational thinking. We’ve also noted the benefits of unstructured time for creativity and for inspiring insightful problem solving as supported by a 2009 study on wandering minds. This week’s blog brings together these two ideas with a look at a puzzle called the Ball of Whacks. This toy was recommended to us by an IMACS alumna whose daughter is enrolled in our Primary Enrichment math class, so we have it on good authority that the Ball of Whacks is a winner!

What Is It?
The Ball of Whacks is a puzzle that consists of 30 magnetic pyramids, which the inventor calls “Whacks.” When you open the package, the 30 pieces are held together by internal magnets in the form of a ball-like, 30-sided rhombic triacontahedron. Give the “ball” a good whack and it will break apart so that you can play with the pyramid pieces.

What makes these pyramid pieces so special? Each is a right golden rhombic pyramid! (We math geeks tend to have a natural appreciation for toys such as this one.) As the mini-book that comes with the Ball of Whacks explains:

Space Out
Whether you’re an aficionado of this special polyhedron or what you’ve read above is enough to satisfy your mathematical curiosity, we think you will enjoy playing with this toy in several ways. After breaking the puzzle apart, your natural first instinct may be to figure out how to put it back together. Although this won’t be challenging for most of our blog readers, we think you’ll still find it satisfying if you enjoy the simple beauty that mathematics often presents.

With that out of the way, you might find yourself casually shifting puzzle pieces around without much physical effort or purposeful direction. Then in what seems like a sudden moment, they come together in one of many interesting shapes or patterns. The experience is reminiscent of doodling as a way of relaxing and unleashing your subconscious. This kind of unstructured play feels uncannily like a physical representation of a wandering mind that experiences sudden insight in solving a problem.

Creative Design
When you’re in the mood to solve a well-defined problem analytically, pick one of the more than 20 shapes in the mini-book and try to make it yourself. Then think outside the book and create your own design. If you enjoy tangrams, then you’ll probably enjoy playing with the Ball of Whacks in this way. Don’t forget that the pyramid pieces are magnetic, so you can create designs on any metallic surface such as a refrigerator door or magnetic white board.

In addition to the shape challenges, the mini-book also contains 15 exercises that make up what is called a “creativity workshop.” For example, Exercise 4 asks you to drop your assumptions about how you play with the Ball of Whacks. As the book explains:

The exercises make for an interesting casual read. They may even help parents begin discussions with children that end up leading to creative thinking. Given that different minds get stimulated by different types of experiences, it’s hard to say definitively that this particular toy will enhance your creativity. However effective the Ball of Whacks is as a creativity tool for a given individual, one thing is certain: the Ball of Whacks is a fun toy for unstructured play, which is widely understood to be good for creativity.

Geometric Gem
The Ball of Whacks can be had for about $25 online through retailers like Amazon. Some might balk at what seems like a high price for a “simple” toy; however this seems to be in line with the price for magnetic “thinking” toys such as Magna-Tiles and Geomags. For a mathematically inclined mind, the Ball of Whacks can be loads of fun!

This scorcher of a summer is only half over. Are your kids bugging you for stuff to do? If you own an iPad, consider these nicely priced apps to keep their minds engaged and entertained. They won’t even realize they’re learning something! We realize this list is hardly complete, so IMACS welcomes your suggestions for similar apps on any platform. The main criteria, which is how we picked these three, is that the app should introduce some type of mathematical or computational thinking in a very natural and intuitive way. No overt instruction. No drilling. Just clever and fun learning!

Cargo-Bot (Free)

Cargo-Bot won’t teach you how to program, but it goes a long way to introducing some of the basic principles of computational thinking in the guise of a fun and addictive game. Each puzzle starts with various colored boxes on a platform and a picture of how the boxes should be situated once the puzzle is solved. Your job is to make the robotic arm move the boxes from their starting position to the prescribed ending position using a set of simple of drag-and-drop commands. The trick is to complete the task using the fewest number of instructions. That’s right, you get more points for shorter programs!

In addition to surreptitiously introducing the basics of stacking, sorting, looping, if-then statements, and calling another program, Cargo-Bot forces you to think carefully about your “code.” You might succeed in moving the boxes to their correct destination, but with anything less than the ideal solution you’ll come up maddeningly short of the maximum stars awarded. Your program might also cause the claw to do something unpleasant like smash into a wall. You simply can’t help but want to remedy these situations. In other words, the app makes you want to debug your code or make it more efficient. Brilliant!

Symmetry Shuffle ($1.99)

Symmetry Shuffle is a visually beautifully app that tests your spatial reasoning abilities. Use your fingertips to slide (translation), flip (reflection), and turn (rotation) an asymmetric master image across a board made up of similar background images positioned with different orientations. See with your mind’s eye and your actual eyes what happens to the master image under these geometric transformations. Each time you move the master image over a background image so that they match in orientation, the monotone background image becomes artfully colorful. Complete all matches to solve a puzzle.

The puzzles can be played in two modes. In Race Mode, you try to score as many points as you can before the clock runs out. One point is awarded each time you make a match. Unused time from the previous level is added to the total time allotted to solve the next level. In Solve Mode, you try to solve the puzzle using the fewest moves. Even the toddler/preschool set could appreciate this game. There is really no need for verbal explanation. The touch commands are so intuitive that a few examples make clear what to do.

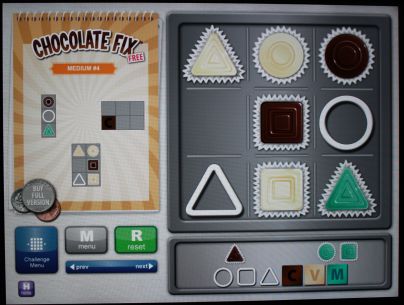
Chocolate Fix Free (Free) and Chocolate Fix ($2.99)

We’re eternal fans of the ThinkFun’s Chocolate Fix game, both the physical version and the app. (Could it be because IMACS alumus Mark Engelberg is the developer?) This perennial favorite of our students makes learning logic so much fun! The rules of the app are the same as the physical game. Color and shape clues offer incomplete information about the location of each confection in a 3×3 tray. Use your logical reasoning skills to determine where each of the nine pieces go.

Chocolate Fix Free contains 30 challenges across four levels of difficulty (15 easy, 10 medium, 3 hard, and 2 expert), whereas Chocolate Fix contains 100 challenges at each level for a total of 400. For the very young or the logic novice, one great aspect of the app is that you can click on the “Hint” icon to get just a bit of help. With the physical game, it’s difficult to get hints because flipping over the challenge card reveals the entire solution on the back.

Enjoy the rest of your summer!

Are you interested in learning to play chess? Is your child? Teen chess champion and IMACS student, Rachel Gologorsky, shares her advice on how to get started. Read more about Rachel’s journey from curious toddler to 2011 US Girls Junior (U21) Chess Champion in her previous blog post.

It’s really easy to be good at chess if you start the right way and with the right foundation. That’s how my father taught me after my mom explained the object of the game and how to move the pieces. He taught me to first focus on the last, i.e., the endgame. If you know where you want to go, the rest becomes easier—it is just a matter of execution.

Endgames

The endgame is the end stage of chess games, commonly defined as when there are fewer than six pieces on the board. There is so much to learn in endgames, but Jeremy Silman’s book, Silman’s Complete Endgame Course, is an excellent tool for learning all the endgame ideas one needs to know from beginner to master.

Focusing first on the endgame is helpful because it highlights how the pieces coordinate together. When there are so few pieces it’s easy, especially for a beginner, to see how each of her moves affects the opponent’s move and how that, in turn, affects her next move.

The first thing that beginners should learn in endgames is how to win, that is, how to put the opponent in checkmate. A checkmate, or “mate” for short, occurs when a king is under direct attack and cannot avoid being captured.

Studying how to put the opponent’s king in mate helps a player to learn the relative power of different pieces and to sharpen her ability to create mating nets. Creating mating nets is the process of methodically restricting the options of the opponent’s king until, at last, the king is put in mate.  These nets are especially pleasing to players with an innate sense of geometry, structure, and neatness. This is because mating nets are usually created by methodically repeating the same geometric structure in a precise move order, leaving nothing to chance in the quest to mate the opponent’s king.

These methodical moves are actually plans, and the concept of plans and planning becomes an engraved tenet in the foundation of the young player’s mind. Later on the ideas of plans and planning become an important component of playing chess strategically.

After I mastered the basic endgame checkmates (how to mate the opponent’s lone king with any of the following combinations: (1) king and queen, (2) king and two rooks, (3) king and rook, (4) king and two bishops, and (5) king, bishop, and knight), my father added another component to our program: tactics.

Tactics

A tactic is a sequence of moves which limits the opponent’s options and may result in tangible material gain. Tactics occur in patterns—the move sequence may be different, but the overall idea is the same. There are many different kinds of tactic patterns, but all are built on the most basic “skeleton” patterns. Those are:

The fork: A fork occurs when a single piece attacks two pieces at once.

The skewer: A skewer occurs when one of your pieces attacks two of the opponent’s pieces in a line, where the more valuable piece is in front of the second piece. The opponent is forced to move the more valuable piece to avoid its capture, thereby exposing the piece behind it, which can then be captured.

The discovered attack: This attack is revealed when one piece moves out of the way of another piece. The discovered attack can be very powerful, as the piece moved can make a threat independently of the piece it reveals. They succeed because the opponent is unable to meet the two threats at once.

Indeed, every one of the above tactics relies on a double threat or a double attack, as it is most commonly called. That is the basic idea of every tactic played, whether the tactic is played by beginners or grandmasters (GM). Indeed, GM Yuri Averbakh, the oldest living GM in the world, stressed in his Chess Tactics for Advanced Players that “the double attack is in one form or the other is [sic] the basis of [even the] most intricate tactical operations.”

Learning and finding these elemental tactical patterns in positions is vital to a player’s development because doing so etches those patterns in the player’s mind. Once you own these patterns, you can recognize them in games. This allows you to turn lost games into winning ones and avoid turning winning games into lost ones.

You can also build on these patterns and combine them to create potent combinations that, over a sequence of moves, force your opponent at the conclusion to lose something. The sequence of moves could force a checkmate, or force the opponent to lose material (valuable pieces or pawns), or force the opponent to give up a strategic asset. Making use of tactics to build up a combination in which I give up all of my pieces but one—the one that forces mate—is beautiful. Those combinations hold an aesthetic value for me, and that makes them fun to see and even more fun to play.

My father always opened our tactics book last so that the end of our chess sessions was always the most fun. Today, however, free websites like Chess Tempo are becoming preferable to tactics books. Not only is there virtually no limit to how many tactical puzzles one can access, the tactical puzzles are chosen on a bell curve with consideration given to your rating. This way, the difficulty of the puzzles grows with your strength.

After I grasped the basic tactical patterns, my father added a completely new dimension to our sessions: strategy. This too, in a way, is working backwards because implementing strategy allows one to coordinate one’s pieces favorably. And when that happens, tactical strikes usually appear that make use of the positions of the pieces.

Strategy

Strategy is the aspect of chess playing that is concerned with the evaluation of chess positions and the setting of goals and long-term plans for future play. Strategy is basically about playing better chess than your opponent and, in chess slang, is called “outplaying the opponent.” Jeremy Silman’s book, How to Reassess Your Chess, is a wonderful guide for learning a logical approach to strategy.

Strategy becomes more important as a player’s skills progress because the players are less likely to miss or be felled by a major tactical blow. Thus, decisive games rely more on which player can outplay his opponent. Outplaying an opponent can only be done with a good grasp of strategic concepts (I still haven’t figured out all of them), some of them being:

Strategy, if implemented correctly, can also be beautiful. Unlike flashy tactics, however, strategy is deep and cannot be spotted easily. Finding strategic ideas and implementing them gives a player a sense of confidence, appreciation of the game, and satisfaction because a win based on strategy means that your opponent didn’t make any mistakes at all—you just outplayed them!

Openings

Finally, my father turned his eye toward openings. An opening is how you start the game and usually lasts for around 10 moves or so. Openings are important in the sense that you want to start a chess game off on the right foot. One has to know openings in order not to lose the game right of the bat.

Nowadays, some of the more advanced players don’t spend much time on openings because they already know the general principles. The most advanced players (grandmasters), however, have to know openings deeply because the slightest inaccuracy will be capitalized on by their opponents. If you’re just starting out in tournament chess, you will most likely play beginners. But even they are becoming more and more “booked up” (i.e., know many opening variations). Although I don’t recommend studying openings too much as a beginner, I do recommend studying the main opening you play enough to know its major guiding idea. That way you can parry any prepared move logically and stay out of trouble.

There are those who will try to catch you in traps. Although better, logical play should and will eventually prevail, it’s useful to know common “trash trap” lines (i.e., a sequence of opening moves that sets a trap for you to fall into, but usually damages the position of the opponent who sets it). You will lose if you don’t see the “trash trap,” but if you know the trap, you will be able to counter it in such a way as to capitalize on your opponent’s damaged position.

It’s good to learn and play mainstream open game openings. Open game openings are characterized by one or more of the following:

(a) Open files (the squares running down a board)

(b) Open diagonals (the diagonals running across the board)

(c) Fluid (easily exchangeable) or absent center pawns (pawns on the e4/d4/e5/d5 squares; Click here for a complete explanation of the algebraic notation used in chess.)

(d) Tactical devices playing a major role

(e) Possibilities of gambits (openings in which one side gives up material for some sort of compensation)

(f) The first move played is the king’s pawn moving two squares forward. (In algebraic notation, the move would be expressed as 1.e4.)

These openings are educationally important because they show clearly many strategic elements, such as methods of:

Openings also highlight elements that have both strategic and tactical components, such as the importance of tempi (the interplay of time and moves), plans, and counterplans. These things are usually explained very well in most opening books. Chess Openings for White, Explained and its companion volume, Chess Openings For Black, Explained do an exceptionally good job of explaining opening ideas.

Practice and Learn

If one is serious about chess one should also play in rated USCF (United States Chess Federation) tournaments, if only to test the ideas out in action and to track progress. Since it’s often impractical to go to tournaments more often than once a month (unless there is a chess club nearby), I recommend either playing games in the meantime on the free ChessCube website, or buying a membership to the Internet Chess Club (ICC, $30 per year). In my experience, ICC has better interfaces, graphics, and is generally easier to navigate and understand than other chess servers. But the main point is that one has to play games often in order to track progress and improve.

As the player’s skills improve and s/he reaches a class D (1200-1400) tournament rating, hiring a private coach can be of an enormous help. My current coach, GM Alexander Shabalov, a four-time US chess champion, has been instrumental in analyzing my games, explaining new opening ideas to me, and pinpointing my weaknesses and misconceptions.

Finally, although Zermelo’s theorem in game theory proves that chess can be “solved” in the sense that the game’s final outcome can be forced, chess is still a game of so many possibilities that understanding its intricacies is a lifelong endeavor. I know that throughout my lifetime, my attempt to understand chess better will be a journey of constant learning. And, that is my goal: to learn all I can, in chess and in the world in general.

Editor’s Note: The IMACS Blog will return on Thursday, July 19th. If you’re celebrating during 4th of July weekend, have a happy and safe time!

Editor’s note: The material below is adapted from ‘Book 0 Chapter 1: Operational Systems’ of the Elements of Mathematics series. The EM series of secondary school mathematics textbooks is a 27-volume collection written and published by the IMACS Curriculum Development Group and serves as a basis for the high-level online math courses available through eIMACS, the distance-learning division of IMACS.

In our previous IMACS blog post on modular arithmetic, we introduced the Clock Game as a fun way to teach children about modular addition. Now, we’ll introduce a few variations on the Clock Game that make it more interesting. If you’re not familiar with the Clock Game, we suggest that you first read our introduction to modular addition before adding on with this post. Have fun!

The Double Game

In the double game, there are two pieces at each number at which to play instead of just one.

The game described in our introduction to modular addition can also be played as a “double game.” The only difference is that when playing double games, a player has more choices. For example, if, as a result of a particular move, a player has to place a checker at a number, one of whose circles is unoccupied and one of whose circles is occupied by the opponent, the player has the choice of either taking the opponent’s checker by replacing it with one of his or her own, or placing a checker on the unoccupied circle and leaving the opponent’s checker on the math. Double games, therefore, last longer, since all the available places must be occupied before the game is over.

Kings and Double Kings

Another variation of the games which can make them more interesting involves the use of kings and double kings. Only one place at each number is used in these games. In this variation, if the move requires it, you may place a second checker on top of one of yours already occupying a particular position, thus creating a “king checker.” If you have a king checker already occupying a certain position, then, if the move requires it, you may place a third checker on top of the king, thus making a “double king.” If a double king occupies a particular position, no further checkers may be added to the pile and so the play continues as in the simplest version of the game.

If your opponent would normally land on a place where you have a double king, then that double king cannot be removed, and the opponent cannot place a second checker. The hour hand, however, should still be moved so as to point at the position occupied by the double king even though your opponent could not place a checker there. If, however, your opponent lands on a place where you have a king, then both your checkers may be removed and replaced by one of your opponent’s checkers. The game ends when all of the positions are occupied by at least one checker upon the completion of a turn. This type of game is scored by counting 3 points for each double king, 2 points for each king, and 1 point for each single checker.

Kings, Double Kings and the Double Game

This variation utilizes the rules of the last two sections simultaneously. The first checker of each move must be placed on an unoccupied position, but there may be several choices for the second checker. For example, suppose your second checker has to be placed at “3,” your opponent has a king on one of the positions labeled “3,” and you have a checker (or a king) on the other position labeled “3.” You may either remove your opponent’s king and replace it with one of your own checkers, or you may form a king (or a double king) of your own. In such a situation, you may always choose either one of the two possibilities offered you by the two positions corresponding to the number at which your second checker is to be placed.

Editor’s note: The material below is adapted from ‘Book 0 Chapter 1: Operational Systems’ of the Elements of Mathematics series. The EM series of secondary school mathematics textbooks is a 27-volume collection written and published by the IMACS Curriculum Development Group and serves as a basis for the high-level online math courses available through eIMACS, the distance-learning division of IMACS.

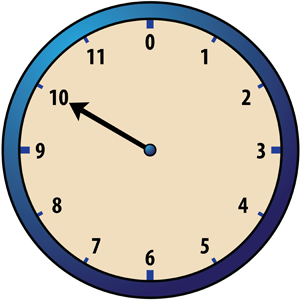
Consider a clock face such as the one shown below:

If the clock shows 10 o’clock, what time will it show 11 hours later? If the clock shows 5 o’clock, what time will it show 12 hours later? If the clock shows 6 o’clock, what time will it show 6 hours later? If you answered 9 o’clock, 5 o’clock and 12 o’clock, respectively, then you’d be right. This exercise suggests a new kind of arithmetic. Let’s call it “clock addition” or, because this kind of addition involves just the numbers 1 through 12, “Clock 12 addition” and denote it by +₁₂. Then the following statements correspond to the three questions above:

10 +₁₂ 11 = 9

5 +₁₂ 12 = 5

6 +₁₂ 6 = 12

Notice that the number 12 plays a very special role in Clock 12 addition. When you add 12 to any of the numbers from 1 to 12, the number remains unaffected. For example, 5 +₁₂ 12 = 5, 12 +₁₂ 12 = 12, etc.

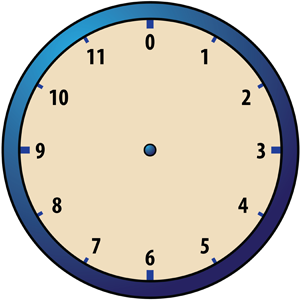
In ordinary addition the number 0 has this property. This suggests that it might be convenient to replace the “12” on our clock face by a “0” so that our clock face looks like this:

With this slight change from the usual clock face, we can now summarize the situation as follows: Clock 12 addition involves the twelve numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11. We denote this set of the numbers by Z₁₂ (read, “Z sub 12”). Here is the rule for computing x +₁₂ y for any numbers x and y in Z₁₂.

For all numbers x and y in Z₁₂, x +₁₂ y is equal to:

x + y, if x + y is less than 12, or

x + y – 12, if x + y is greater than or equal to 12

In plain English, that means: To find the Clock 12 sum of x and y, first find the ordinary sum of x and y. If this ordinary sum is less than 12, you are finished – the Clock 12 sum is just the ordinary sum. On the other hand, if the ordinary sum is greater than or equal to 12, then subtract 12 from the ordinary sum to get the Clock 12 sum.

Notice that in any case, as long as x and y are in Z₁₂, x +₁₂ y will also be in Z₁₂. (Can you prove that?) Since for any numbers x and y in Z₁₂, the Clock 12 sum, x +₁₂ y, is again in Z₁₂, we call +₁₂ an “operation” on Z₁₂. Similarly, ordinary addition is an operation on the set of all natural numbers, N, which consists of the numbers 1, 2, 3, … . On the other hand, ordinary addition is not an operation on Z₁₂, and ordinary subtraction is not an operation on N. (What are some examples that support this statement?)

We have been calling +₁₂ “Clock 12 addition” because it’s very closely related to the kind of adding you do on a real clock. The operation +₁₂ is also called “addition modulo 12” or “addition mod 12” for short.

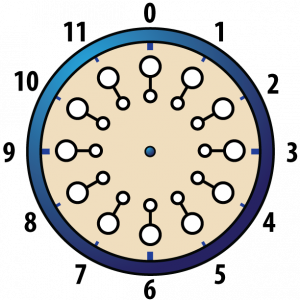
Clock 12 Addition Game

Now we’ll describe a game called “Clock 12” that two players, A and B, can play on a circular board. You’ll need a movable arrow for the hour hand so that your game board looks like the figure below.

Player A begins the game by placing a checker on one of the twelve numbers around the edge of the clock face. The hour hand is placed so that it points at the number on which the checker has been placed. The corresponding time is called “the hour.” For example, if Player A puts a checker on 10, the hour hand is placed so that it points at 10. Player A then says “The hour is 10 o’clock.”

Player B makes a move in two stages: first by placing a checker of a second color on one of the unoccupied numbers, and then by placing a second checker of the same color in such a way that the following is true: The starting hour plus (mod 12) the number of hours corresponding to Player B’s first checker is equal to the time corresponding to Player B’s second checker. The arrow is then made to point at the number on which Player B’s second checker was placed, thus indicating the new hour. Player B then declares the new hour.

Example 1
Suppose Player A begins the game by placing a checker on 10. Then the hour is 10 o’clock. If Player B chooses 4, then his or her first checker is placed on 4, and the second checker is placed on 2 because 10 +₁₂ 4 = 2. The hour hand is then moved to 2 o’clock.

Example 2
Suppose Player A chooses 0. If Player B chooses 4, the first checker is placed on 4. In this case, 0 +₁₂ 4 = 4, and Player B already has a checker on 4. Therefore, there is no need to place a second checker on 4, and so Player B’s turn ends with the hour being 4 o’clock.

Example 3
Suppose Player A chooses 10 and Player B chooses 0. Then, since 10 o’clock plus 0 hours is 10 o’clock, Player B’s second checker ought to be placed on 10. However, Player A’s checker is already on 10. In this situation, Player B takes Player A’s checker and replaces it with one of his or her own. The hour hand, which was pointing to 10 before Player B’s move began, will not be changed. The hour is still 10 o’clock.

The players continue to alternate turns using rules described in the examples above. If, after completing his or her turn, a player leaves the board so that there are no more unoccupied numbers, then the game is over and the player with the most checkers on the clock wins!

My earliest memory of chess was from when I was around three years old. I remember sitting on the edge of a rug playing with colorful LEGO blocks. When I looked up, I saw my father and my oldest brother playing chess. The board was illuminated so brightly that it looked as if the pieces were shining. I looked back down at my blocks, and they seemed so boring compared to the multitude of pieces and squares and interesting stuff happening on the board above. That was when I was first aware of my desire to play on that board and with those pieces. I would crawl over to where my father and brother were playing, take a few game pieces, and put them on the board too. After “playing” with them a few times in this way, I was henceforth banished from the vicinity of their games. This continued for two years until my mother determined that I had the capacity to understand what was going on. However, nobody believed her, so she taught me the basics herself. It took me about a week to grasp those rudiments of chess, after which I was handed over to my father for further instruction.

My father and I would take a chess set and chess book from our library at home and bike to one of our favorite places. There, my father would set up a position from the book on the board, and we would puzzle it out together. In the beginning, we would actually move the pieces, but after a few weeks my father urged me to work out the entire solution and move the pieces only in my head. We studied tactics, strategy, endgames, etc. I gradually improved to a stage where I could have a “reasonable” game with him (“reasonable” in the sense that I wasn’t losing after the fourth move). A few years later, when I was eight or so, I learned that there was a chess club at a local elementary school, so naturally I went to check it out. There I found good competition with kids my age and with one boy in particular. We were about evenly matched, so when he went to a tournament and won a big trophy, I wanted one too! That’s how I got started with tournaments.

For a few years though, competition took a back seat to other important family events, which had the strange habit of conflicting with tournament schedules. School was also a factor: It would have been difficult to actively study chess and play in tournaments given all the classwork and homework I would have had to make up for the days I missed. Also, tournaments usually run through Sunday, and my Sundays were taken up with IMACS. I loved IMACS so much that I wasn’t willing to skip even one class if I could help it. When I was in third grade, my parents withdrew me from the school I was attending for a variety of reasons, including lack of a challenging curriculum that kept me perpetually bored even though I skipped a grade. I was homeschooled while my parents searched for another school, and I recognized this as an excellent opportunity to have a say in my education. I was on my best behavior for months before I convinced my parents to homeschool me forever! Now that I was homeschooled, I had loads of free time. Also, my IMACS classes were moved to Thursday. So, now that I had the time and was not sacrificing IMACS, I got interested in competitive chess again.

From my friends at tournaments, I found out about the Internet Chess Club (ICC). With my new ICC membership, I played for hours after my studies were done (which at 3rd grade took a grand total of an hour and a half). My parents always encouraged me to play up (i.e., at a higher level), so already in elementary school I was regularly playing up in K-12 events. This wasn’t very good for my rating as I usually lost many games, but as a consolation, from age 8 on, I was Florida’s Top Girl at the K-12 level for several years in a row. At that time, Women’s World Champion Grandmaster, Alexandra Kosteniuk, was handing out the Florida’s Top Girls prize. After a few years of shaking hands with her, my mom asked her to coach me. I improved dramatically under Alexandra’s guidance – I developed an opening repertoire, whereas before I usually made up my own openings (that sometimes didn’t turn out well). As my rating shot up, I made the Susan Polgar’s National Team for Girls and was invited as the representative from Florida to play in her 2009 National Invitational for Girls event. That was my introduction to girls-only events. I took second place, and made new friends. My mom is always checking the Web site for FIDE (the World Chess Federation, or Federation Internationale des Echecs). There she found out about the 2010 North American Youth tournament. The fact that one of my new friends was going to attend helped seal the deal. We were both US representatives, and it felt awesome to tell people that I was representing the United States of America. A series of wins and draws took me to the final round where I ultimately won! And so in my first international tournament I got my first gold medal for the US. As I hadn’t been having great results before that tournament, the win was welcome and kept me studying chess even with my increasing workload. (Studies at my age now aren’t as easy as in 3rd grade!)

My coach, Alexandra, started a family, which meant that she rarely traveled from her home in Russia to the US anymore. Thus, my parents decided to choose a different coach to fill in the gaps – four-time US Champion and Grandmaster Alexander Shabalov. Under his guidance I won the 2011 US Girls Junior (U21) Chess Championship this past August with an undefeated score. Whenever I’m feeling low, there always comes a win to keep me motivated. Chess is an amazing game, and I’m very competitive, so that also always brings me back to competitions. I love playing and seeing how I stand against some of the big names in chess (or more often, those who say they’ve played them). My favorite competitions are the one day tournaments, because I get to go home quickly. The longer 6-7 day tournaments, like the Susan Polgar, North American Youth, and the US Junior Girls leave me homesick toward the end. (For how long can one eat hotel food?) Now I’m in a lull between tournaments, so I practice by playing on ICC and chesscube.com for about an hour each day. My next big tournament will be the World Youth Chess Championship in Caldas Novas, Brazil, this November where I will represent the United States.

This week, IMACS catches up with an old friend, Mark Engelberg. Mark was part of the inaugural class of Project MEGSSS students in Broward County, Florida, when that program began in 1983. MEGSSS (Mathematics Education for Gifted Secondary School Students) was an ambitious public school course of study with a curriculum designed specifically for the brightest math students. The Broward program became IMACS in 1993. Like many of his fellow MEGSSS/IMACS alumni, Mark went on to an accomplished career in a STEM-related field. He is known for having designed the bestselling logic game, Chocolate Fix, as well as adding thousands of new challenges to the popular Rush Hour game.

How did Chocolate Fix evolve from an idea to a bestselling game to the basis for a new logic curriculum?

Chocolate Fix started out as a product called Gridworks. Gridworks was my first collaboration with ThinkFun, and its creation was very much a team effort. Bill Ritchie, the CEO of ThinkFun, had the initial inspiration to build a visual logic puzzle system. I proposed the pattern-matching framework for the clues and made the case that such a system would be simple, elegant, and expressive. Two very brilliant and prolific puzzle designers, Serhiy Grabarchuk Jr. and Scott Kim, ran with the idea and came up with the initial book of 60 puzzles. And of course, ThinkFun’s excellent artists and graphic designers came up with the product’s look and feel. It was a real thrill to work with so many talented individuals.

The funny thing, looking back, is that at the time, we weren’t entirely certain whether such a clue system would be rich enough to create challenging and interesting puzzles. Yet nearly a decade later, we haven’t even come close to exhausting Chocolate Fix’s potential; we’re constantly discovering clever new types of puzzles that can be expressed within the system.

Meanwhile, Chocolate Fix received the Parents’ Choice Gold Award in 2008, and in 2010, the Bunge Lab at UC Berkeley published a study that named Chocolate Fix as one of a handful of puzzle games that were shown to increase IQ. We know of at least one geometry teacher who has successfully used Chocolate Fix to teach his students the skill of constructing mathematical proofs. This is all exciting stuff, and it looks like Chocolate Fix has a bright future. Right now, we’re looking at ways to combine all the things we’ve learned about Chocolate Fix and turn it into an actual curriculum for teaching logic, problem solving, and mathematical proof skills.

You were also instrumental in using technology to develop thousands of new challenges for the Rush Hour app when the initial thought was that all the “good” challenges were gone. What are your thoughts on how technology continues to affect how we play games?

Technology touches every facet of our lives, and games are no exception. Computer games, for example, now form one of the largest segments of the entertainment industry. Even when it comes to non-electronic games and puzzles, computers play an important role behind the scenes. Nearly every crossword puzzle and sudoku are created these days with the assistance of computers. Artificial intelligence programs continue to shed new light on strategies for the world’s deepest games, including Chess, Go, and Poker. So to me, it seemed perfectly natural to apply my programming skills to the task of creating fresh new Rush Hour challenges.

You are the inventor of two other games – Animalogic and Snorkels. Tell us about them.

Animalogic received the Parents’ Choice Gold Award in 2009. Like Chocolate Fix, it is a solitaire puzzle system that comes with a book of challenges. The premise is that you have to successfully get 16 colored animals across a river, but the animals will only line up behind other animals that match in type or color. It’s a nice spatial, attribute-matching puzzle system with simple rules that even the youngest of kids can understand, but the puzzle book has a full range of difficulty levels, including expert challenges that will give adults a mental workout.

Snorkels is a two-player strategy game where each player controls a team of cute, colorful aliens with the goal of being the first to capture one of your opponent’s aliens. The capturing mechanism in Snorkels comes directly from the ancient Asian strategy game Go, which is widely regarded as the deepest strategy game ever devised (even deeper than Chess!). In fact, I created Snorkels primarily to be a “gateway game” to Go, which happens to be my favorite game. Snorkels is satisfying in its own right, but once you master Snorkels, you’ll find it a snap to learn and enjoy Go.

You recently said that the MEGSSS program, which is now part of the IMACS curriculum, gave you the logical thinking skills that enabled you to develop Chocolate Fix. Can you elaborate on that?

When creating the clue system for Chocolate Fix, I was heavily inspired by my experience with Book 1 of the Elements of Mathematics series, “Introductory Logic.” [Editor’s note: This material now forms the Logic for Mathematics I (LM1) curriculum at IMACS.] In a strong sense, each proof challenge in EM Book 1 is a kind of puzzle, and I wanted to capture that kind of thinking in Chocolate Fix. The partial grid clues are a form of disjunction, and the ability to put multiple constraints within one pattern are a kind of conjunction. (Gridworks also featured negative clues. We removed them from Chocolate Fix to simplify the system, but we hope to bring them back as part of the curriculum we’re developing.) When solving a challenging Chocolate Fix puzzle, you can expect to use Inference by Cases, Indirect Inference, and other techniques now taught in the LM1 course at IMACS.

Describe your career path from when you graduated from MEGSSS to your current work in puzzles and games and curriculum development. Who or what experiences influenced you along the way?

After MEGSSS, I went to Rice University, where I double-majored in Computer Science and Cognitive Sciences. From there, I programmed virtual reality simulations at NASA, and then got into the computer game industry, working at Sierra On-line and Rad Game Tools. These days, I’m primarily a stay-at-home dad, but I continue to dabble in puzzles and games when I have spare time.

With respect to puzzles and games, my biggest influence is my own childhood. I logged a lot of hours playing computer adventure games, solving puzzles in GAMES Magazine, and playing boardgames with friends. I was fortunate in college to find a group of friends with similar interests, and I ended up learning a lot about puzzle construction through our many conversations and brainstorming sessions about what worked and what didn’t. I try to create the kinds of things I would have enjoyed when I was in middle school.

If someone reading this thinks he or she has the next brilliant idea for a game or puzzle, what should he or she do next?

The beauty of the Internet age is that it is so easy to get your idea out there. Learn how to program so you can put together a mobile or Web app to showcase your idea.

Build your future on a solid IMACS foundation. Take our free aptitude test today.

In the third and final part of our summer series on thinking games, we look at three strategy games that are deceptively simple. We use these games at IMACS to sharpen the critical thinking skills of our students. While chess is rightfully considered by many as the ultimate strategy game, we like the three games below because the simple rules are very easy to learn, even for someone as young as five or six, and each game does not take an eternity to play. Best of all, each is kid-tested and IMACS-approved!

Quoridor by Gigamic

Game Essentials: Quoridor is a fantastic game of strategy, especially for those who like mazes. In the typical two-player setup, the pawns are placed on the middle squares of opposite sides of a 9×9 board. The winner is the first to maneuver her pawn from its starting position to any of the nine squares on her opponent’s side. Generally speaking, you can move one square at a time, forward or backward or left or right but usually not diagonally. You can also jump over your opponent’s pawn when the two pawns are face to face. Seems trivial so far, right? That’s because we haven’t yet discussed the fences! You see, at each turn, a player can choose to either move her pawn or to impede her opponent by putting up a fence that blocks or lengthens the opponent’s path. Twenty fences are divided evenly at the start of the game, and the main rule governing them is that you can’t use them to block all possible paths – there must be at least one way to get from one side of the board to the other. The video below from Gigamic illustrates these rules:

For brevity’s sake, the video showed a short and simple game. But, in fact, games are typically much more complex. With each fence placed on the board, an increasingly complicated maze of paths from one side to the other is built. And the results can be downright maddening! One minute, you think you’re making good progress only to have your pathway dead-ended by your opponent, in which case you have to backtrack, costing precious moves. Another time, you may turn the tables on your opponent by blocking him only to be obstructed by your own fence placement later in the game.

As with most abstract strategy games, winning depends on your ability to think ahead about the possible outcomes of available moves and select the optimal path. In other words, to take your strategy beyond simply “move forward – block opponent,” you must build and analyze a decision tree in your mind. You also need to think offensively and defensively at all times. For example, if you are progressing alongside a series of fences, your opponent will almost certainly use a new fence to block you just as you get to an opening. However, if you use one of your fences to block the path behind your pawn, then your opponent may not be allowed to block your way forward if it would close off all paths. Still, you must be careful to use your fences judiciously so that you don’t run out of them too soon.

Quoridor may also be played with three or four players. Each player selects one of the four sides of the board as the side for his pawn’s starting position and works toward being the first to reach the opposite side. Divide the fences up so that each player has an equal number with as few left over as possible. Then just follow the rules of movement and fence placement from the two-player game.

Recommended Age: The manufacturer suggests ages 6 and up, and we tend to agree. The rules of play are simple, but it does take a certain level of maturity to keep from getting frustrated when your opponent repeatedly blocks off your path.

Brain Play-To-Price Ratio: Quoridor lists for $29.99 but can be found for around $23. The rules and objective are easy for the youngest or most inexperienced players to learn, but mastering the game is a fun challenge that will engage children and adults alike for many years. As with most Gigamic board games, Quoridor is made of sturdy wood. And under Gigamic’s 10-year warranty, all you have to do to get free (love it!) replacement game pieces is send a letter to Gigamic.

Easier Adaptation: Gigamic makes a version called Quoridor Kid for ages 5 and up that costs about $5 less. The board is 7×7 instead of 9×9, and there are 16 fences instead of 20. The neutral-color game pieces and board are replaced by cute little mice, colorful fences and a cheerful board. Each mouse has a different colored nose which matches one of four colored cheese wedges on each side of the board. This nose-to-cheese match helps keep little ones focused on exactly which side of the game board they are aiming to reach. The smaller board typically means that a game of Quoridor Kid lasts a shorter amount of time. But the game rules are the same as Quoridor, and thus encourage the same kind of strategic thinking, albeit with a smaller number of paths to consider. The choice between starting with Quoridor Kid or going straight to Quoridor depends on whether you think your child would be more willing to stay engaged with the game due to the cute mouse-and-cheese theme. After all, you could just use the inner 7×7 section of “grown-up” board by ignoring the edge squares, as well as four of the fences.

Noteworthy: You can sample Quoridor online before deciding on a purchase. Just know that manipulating the fences online is not nearly as natural as when you’re holding the real thing in your hand.

Quarto by Gigamic

Game Essentials: Quarto is a two-player game that comes with 16 solid wood pieces and a sturdy 4×4 wooden board. All pieces not yet placed on the board are available to each player. The object of the game is simple: Be the first player to get four pieces that share a common feature in a line and call out “Quarto!” The line can be horizontal, vertical or diagonal, and you do not have to have placed all four pieces on the board yourself. So what are the possible common features? There are eight: a game piece can be light or dark, circular or square, short or tall, and hollow or solid. (A little elementary combinatorics confirms that we should, indeed, have 16 unique game pieces.) Here’s the kicker that makes Quarto stand out from other N-in-a-row games – you don’t pick the pieces that you place on the board; your opponent does! The following video illustrates these rules:

Quarto hones the mind’s ability to recognize patterns. This simple twist of picking out your opponent’s pieces comes with great responsibility for you must take care not to literally hand him the win. If you see that there is already a line with three circular pieces, then choose a square piece for him. If you’ve set yourself up to win with a short piece, then you might try to force your opponent to hand you one by giving him all the remaining tall pieces to play, assuming that such a move doesn’t give him the win.

As with games like tic-tac-toe or Connect Four, a primary strategy with Quarto is to set up more than one possible way to win so that if your opponent blocks one, you can still try to win with another. The ultimate two-pronged approach is to build two lines around two opposing features, e.g., one line of light pieces and another line of dark pieces. Then no matter what piece your opponent hands you next, you’re guaranteed a win because the piece you get, in this example, has to be either light or dark.

Recommended Age: The manufacturer suggests ages 6 and up, but a bright kindergartener should be able to enjoy this game. The rules are very simple. The only thing that takes getting used to is having your opponent choose the pieces that you place on the board instead of selecting them yourself.

Brain Play-To-Price Ratio: Like Quoridor, Quarto lists for $29.99 but can be found for around $23. If you want to experience either game for less, look for the travel editions. The craftsmanship is still excellent, but the smaller size will save you at least another $5. Quarto is fun for all ages, and Gigamic’s 10-year warranty and generous replacement policy applies to it as well.

Multipurpose: For small children, the wood pieces make for obvious fun as building and balancing blocks to hone fine motor skills. But you can also use them to introduce Venn diagrams. Just draw two large overlapping circles on a piece of paper and decide what characteristic each circle represents. For example, one circle can be tall pieces and the other circle can be hollow pieces. Ask your child to place each of the 16 pieces in the appropriate area of the paper. Change up what the circles represent and do it again. Add a new characteristic and expand to three overlapping circles. Not enough room on a sheet of paper? Get some yarn or raid the belts in Dad’s closet and make overlapping loops instead.

Easier Adaptation: With younger or less experienced players, you can simplify the objective by using just one, two or three of the four characteristics to make a winning line. For example, the first person to get four of the same color or four of the same shape in a line wins. Forget about height and hollowness until players feel ready to add on another level of difficulty.

Noteworthy: The Quarto rules also suggest a variation for advanced players that allows for nine more winning configurations. Specifically, in addition to getting four pieces in a line, you can win by getting four in a square. Just try keeping your eyes on all those possibilities!

Othello by Mattel

Othello, also known as reversi, is a widely-played classic game of strategy that has been around in some form since the late 1800’s. Its trademarked slogan sums it up beautifully: “A minute to learn, a lifetime to master!”™ With its simple rules, Othello can be played by children as young as five, even though the recommended age is eight to adult. If you’ve never had the pleasure of playing this game, watch the video explanation below:

Othello is an ideal game for teaching one of the key elements of strategy games, which is to think longer-term even if it means not choosing a move that seems optimal in the short-term. If you approach each turn with the goal of maximizing the number of disks of your color at the end of that one turn, then you will surely lose. Experienced players focus, instead, on setting up “helper” positions that will lead to the capture of certain prized locations on the board. These coveted spots (e.g., corners and edges) give a player tremendous leverage during the last series of moves that take place toward the end of a game.

Given the age and popularity of Othello, it should come as no surprise that its game strategies have been extensively researched, analyzed and documented. Here is a fairly readable strategy guide from the French Othello Federation. You can appreciate from this and other Othello guides that pattern recognition, another key element of strategy games, is an essential skill for winning.

Othello lists for $11.99, and will provide many hours of game play for the whole family. It’s also commonly available as a smartphone or tablet app and online. If you’d like to see some of the best Othello players in the world compete, you are somewhat in luck because the 35th Annual World Othello Championship will be held in the US this year.

If you are just discovering this blog, check out Part One of the series on logic games and Part Two on visual-spatial games. We hope that, through this series, you have discovered a new game or two to keep your brain active during these summer months and for years to come.

Make the right move with IMACS. Sign up for our free aptitude test. Play along with our weekly IMACS logic puzzles on Facebook.

In Part Two of our summer series on thinking games, we focus on those that exercise the brain’s visual-spatial abilities. The three games we recommend below will have you shifting, flipping, and rotating objects in your mind and sharpening your problem solving skills.

Katamino by Gigamic

Game Essentials: Katamino is a versatile tiling game that will put your spatial reasoning abilities through a serious workout. The game comes with 12 three-dimensional pentominoes, eight smaller support pieces, a grid-based board, and a booklet full of challenges. A pentomino is simply a shape consisting of five congruent squares that are connected at their edges. In the case of Katamino, each of the 12 main pieces consists of five congruent cubes that are connected at their faces. Gigamic calls these “pentaminos.”

There are variations on how to play, but in the standard solitaire approach, the object is to neatly place a subset of the pentaminos in a rectangular section of the board. If your goal is to tile N pentaminos (a “Penta N”), then the section will be an Nx5 rectangle. A player typically starts with a Penta 3 challenge. Once it is solved, the player adds another pentamino to the mix and rearranges the now-larger set of four pieces to solve the Penta 4. Next is a Penta 5, a Penta 6, and so on. The puzzles get progressively harder as you add pentaminos.

Another neat way to play is to select one of the pentaminos and then use nine of the remaining 11 to create a larger version of the first one that you chose. This can be done for every pentamino. Challenge yourself to replicate all 12. There are 3-D challenges as well where a player uses the pentaminos and support pieces to build the three-dimensional objects pictured in the booklet. Mathematically speaking, the standard Katamino game is two-dimensional but played with three-dimensional pieces for practical purposes. We imagine that flat pentominoes that are hard to pick up would make the game incredibly frustrating to play, not to mention how fragile they would be in little hands.

Katamino may also be played as a two-player game. In the speed game, players evenly divide 10 of the 12 pentaminos (all except for the “I” and the “X”) and all of the support pieces. The opponents then race to see who can tile his or her half of the board first. The strategy game uses only the 12 pentaminos and an 8×8 board included in the booklet. Each player takes a turn placing a pentamino anywhere on the board. The last player to place a pentamino on the board wins.

Recommended Age: The manufacturer suggests ages 3 and up, and we couldn’t agree more. With its colorful wooden blocks, this is just the kind of game to captivate and stimulate young minds. Kids can’t help but be enticed by the colorful assortment of shapes that almost seem to call out, “Build something with me!” And with the eight smaller support pieces, even three-year olds can enjoy the challenge of tiling without any guidance.

Brain Play-To-Price Ratio: Katamino lists for $29.99 but can be found for around $22. There are 500 challenges included in the accompanying booklet, so children and adults of all ages will have no trouble finding puzzles with just the right level of difficulty. After solving the challenges that come with the game, see if you can enumerate additional challenges. This should keep you busy for a while as there are literally thousands more. This is a well-constructed game made of solid wood that will last through lots of rough and tumble play. And kudos to Gigamic for recognizing that a solid wood game, with its extra heft, needs a reinforced box for storage. When your child passes Katamino down to your grandchildren, it won’t be in a box that looks like something out of “The Mummy.”

Multipurpose: Katamino is a great game with which to introduce concepts from Euclidean geometry. Don’t be afraid to use mathematically precise terms such as “polygon” when playing with a child who has not studied the subject. Start by assuming that the pieces are comprised of unit cubes and explain what that means. Then show how to compute the perimeter and area of each face as well as the volume of each shape. Flip and turn the shapes to demonstrate the concept of symmetry. Which pieces have reflective symmetry, and what are the lines of symmetry? Which pieces have rotational symmetry, and what is the order of the rotation?

Another two-player variation is to play a game of balance by using the blocks to build a stack. Each player takes a turn placing one block on the stack. Whoever is last to place a piece on the increasingly unstable stack without causing it to topple is the winner. This is a great way to sneak in some basic principles of Newtonian physics.

Easier Adaptation: Gigamic makes an easier version called Winomino that includes six of the 12 pentaminos and ten additional pieces that are formed by one, two, three, or four cubes. The smaller pieces allow greater flexibility in solving the Penta challenges. The prices for Winomino and Katamino are about the same. If your child is older or is a natural visual-spatial thinker, then we suggest bypassing Winomino and going straight to Katamino.

Noteworthy: Pentominoes belong to a more generic class of shapes called polyominoes, so named to be consistent with the two-square shape of the well-known domino. Use four squares and you get a tetramino, which is the basis for the popular 80’s video game, Tetris. You can play Tetris online.

Shape By Shape by ThinkFun

Game Essentials: In this variation on the traditional tangram puzzle, 14 puzzle pieces must be arranged in a square tray to match the pattern on one of 60 challenge cards. Six orange pieces form the foreground image, and eight yellow pieces form the background. The orange pieces consist of identical pairs of each of the following: square, parallelogram, and isosceles right triangle. The yellow pieces consist of identical pairs of each of the following: right trapezoid, isosceles trapezoid, swallowtail flag, and a five-sided polygon that resembles a boot. To solve a puzzle, a player must place all 14 pieces neatly inside the puzzle tray with no leftovers and no pieces sticking up.

Anyone can try to solve the puzzles by placing the pieces in a haphazard way without much thoughtful planning. In our observations this usually results in more frustration than solutions, and that’s no fun. The real visual-spatial brain exercise and enjoyment comes when you take the necessary time to really think about where each puzzle piece should go. And it’s these mental gymnastics that can improve a person’s ability to handle visually intensive tasks from planning the seating at a wedding reception to designing pharmaceutical drugs to guiding a space-walking astronaut through a complex and unexpected situation from down here on Earth.

While the Shape By Shape challenges are not ranked by level of difficulty, some are definitely easy and others much harder. Take a look at the dog and cat patterns below, and you’ll see what we mean.

The Sad Dog in Challenge 12 is symmetric about the diagonal from top to bottom. Though not always the case, challenges with symmetric images often have solutions that require symmetric placement of the puzzle pieces. Furthermore, the pieces in the dog pattern do not share many edges, so it’s easier to recognize the shapes of individual pieces because they are not part of a larger area made up of connected pieces. For example, the eyes of the dog are obviously the two parallelograms while the nose is clearly one of the triangles. The two yellow areas that are shaped like the swallowtail flags pieces can only be made by those two pieces. Going outward from the eyes to the left and right corners, the yellow areas are most certainly the two “boots”. Once these obvious pieces are put in place, the placement of the other pieces becomes trivial.

By contrast, the Sleeping Kitty in Challenge 14 is asymmetric in every direction, and the pieces in the orange area share a lot of common edges that are in the interior of the cat shape. In kid-speak, the orange pieces are in one big blob. A more mathematical way of putting it would be that the ratio of the area of the cat to its perimeter is relatively high. The same observations can be made about the yellow area. Generally speaking, the higher this area-to-perimeter ratio, the harder the challenge because your visual-spatial brain function has to sort through more combinations of pieces in order to replicate the pattern.

Recommended Age: The manufacturer suggests ages 8 and up, but we think this is an ideal puzzle for much younger kids. Children who are not ready for the puzzle’s pre-defined parameters still stand to gain from the exploratory learning that just naturally happens through play. As a recent academic study indicated, Euclidean geometry is so intuitive that tribal children with no formal education in the subject understand its basic principles.

Brain Play-To-Price Ratio: Shape By Shape lists for $14.99 but can be found at a slight discount. Even at full price, we think this game is a great value. As with all the ThinkFun games we’ve played, Shape By Shape is made with high-quality plastic that’s built to last. The puzzles and the number of puzzle pieces are at just the right level to be challenging but not frustrating for players of all ages and abilities. Sixty puzzles will keep you busy for while, especially if you commit to not looking at the hints on the back of the challenge cards, and you can enjoy the same puzzles again after taking a break. But one of the many cool things about Shape By Shape is that you can challenge yourself to discover new patterns not included with the game. Freestyle play is the one time when starting off with totally random placement is justified. Just go with it and see where it takes you. If you manage to fit all the pieces in the tray, check your pattern against the challenge cards and see if you’ve found a new one. If you’re really ambitious, try articulating the mathematical limits of the shape combinations that would fit in the tray.

Multipurpose: Shape By Shape is another game that is perfect for exploring geometry. Try explaining geometric concepts when discussing observations like the following: The perimeters of the parallelogram and isosceles right triangle are equal, and the perimeters of the isosceles trapezoid, swallowtail flag, and “boot” are equal. The side of the square is equal in length to the shorter diagonal of the parallelogram. It’s also equal to the line segment perpendicular to the triangle’s hypotenuse that connects the right angle vertex and the hypotenuse. Which angles are acute, and which are obtuse? The orange pieces are of equal area, and the yellow pieces are of equal area that is 50% greater than the area of each orange piece. (Can you prove these statements about area rigorously? If not, at least convince yourself visually.) We could go on and on, but you get the point.

Easier Adaptation: A two-part solution is given on the back of each challenge card. If you are working with a younger player, use the first hint to place some or all of the orange pieces. Then go back to placing the yellow pieces without help from the second hint. Unless, of course, you both get stuck and need the second hint. But don’t give up too soon!

Noteworthy: Shape By Shape is one of six ThinkFun games invented by master puzzle designer Nob Yoshigahara. You can read about his work on ThinkFun games here.

Rubik’s Cube by Hasbro

This iconic puzzle has been a part of international popular culture since 1980 when mass-distribution outside of Hungary, home of inventor Erno Rubik, began. We won’t spend much time describing it here. If you really haven’t heard of the Rubik’s Cube, you can explore the official Web site or the many online videos documenting the culture of speed cubing. Here’s one pulled from the oldie-but-goodie shelf. It’s a real throwback, especially for those who remember the 80’s TV show “That’s Incredible.”

Note that the first contestant introduced during the in-studio competition, Holden Thorp, is now the chancellor at UNC Chapel Hill after having earned his PhD in chemistry from Caltech and going on to receive the NSF’s Presidential Young Investigator Award among his many accomplishments.

Robots also enjoy the challenge of the Rubik’s Cube, or at least their human engineers do. You can watch and read about the robot that currently holds the speed record here.

For algebra aficionados, check out these two papers and a book relating group theory to the Rubik’s Cube:
• Group Theory and the Rubik’s Cube by Janet Chen
• Group Theory via Rubik’s Cube by Tom Davis
• Adventures in Group Theory: Rubik’s Cube, Merlin’s Machine, and Other Mathematical Toys by David Joyner

In our opinion, this little gem should be part of every child’s collection, although you should keep it away from little ones due to the small mechanical parts that can be removed. The original 3×3 Rubik’s Cube lists for $11.99 but can often be found for $8 or less. That’s dirt cheap these days for a cool thinking toy that’s also part of history. But if you’re just not into playing games in the physical world anymore, you can still test your Rubik’s solving skills here.

If you missed Part One on logic games, read it here. See you next week for Part Three on strategy games!

Visualize your future with IMACS. Take our free aptitude test. Follow IMACS on Facebook.