Editor’s note: The material below is adapted from ‘Book 0 Chapter 1: Operational Systems’ of the Elements of Mathematics series. The EM series of secondary school mathematics textbooks is a 27-volume collection written and published by the IMACS Curriculum Development Group and serves as a basis for the high-level online math courses available through eIMACS, the distance-learning division of IMACS.
Consider a clock face such as the one shown below:
If the clock shows 10 o’clock, what time will it show 11 hours later? If the clock shows 5 o’clock, what time will it show 12 hours later? If the clock shows 6 o’clock, what time will it show 6 hours later? If you answered 9 o’clock, 5 o’clock and 12 o’clock, respectively, then you’d be right. This exercise suggests a new kind of arithmetic. Let’s call it “clock addition” or, because this kind of addition involves just the numbers 1 through 12, “Clock 12 addition” and denote it by +12. Then the following statements correspond to the three questions above:
10 +12 11 = 9
5 +12 12 = 5
6 +12 6 = 12
Notice that the number 12 plays a very special role in Clock 12 addition. When you add 12 to any of the numbers from 1 to 12, the number remains unaffected. For example, 5 +12 12 = 5, 12 +12 12 = 12, etc.
In ordinary addition the number 0 has this property. This suggests that it might be convenient to replace the “12” on our clock face by a “0” so that our clock face looks like this:
With this slight change from the usual clock face, we can now summarize the situation as follows: Clock 12 addition involves the twelve numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11. We denote this set of the numbers by Z12 (read, “Z sub 12”). Here is the rule for computing x +12 y for any numbers x and y in Z12.
For all numbers x and y in Z12, x +12 y is equal to:
x + y, if x + y is less than 12, or
x + y – 12, if x + y is greater than or equal to 12
In plain English, that means: To find the Clock 12 sum of x and y, first find the ordinary sum of x and y. If this ordinary sum is less than 12, you are finished – the Clock 12 sum is just the ordinary sum. On the other hand, if the ordinary sum is greater than or equal to 12, then subtract 12 from the ordinary sum to get the Clock 12 sum.
Notice that in any case, as long as x and y are in Z12, x +12 y will also be in Z12. (Can you prove that?) Since for any numbers x and y in Z12, the Clock 12 sum, x +12 y, is again in Z12, we call +12 an “operation” on Z12. Similarly, ordinary addition is an operation on the set of all natural numbers, N, which consists of the numbers 1, 2, 3, … . On the other hand, ordinary addition is not an operation on Z12, and ordinary subtraction is not an operation on N. (What are some examples that support this statement?)
We have been calling +12 “Clock 12 addition” because it’s very closely related to the kind of adding you do on a real clock. The operation +12 is also called “addition modulo 12” or “addition mod 12” for short.
Clock 12 Addition Game
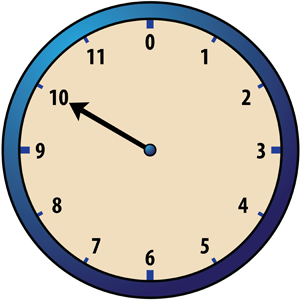
Now we’ll describe a game called “Clock 12” that two players, A and B, can play on a circular board. You’ll need a movable arrow for the hour hand so that your game board looks like the figure below.
Player A begins the game by placing a checker on one of the twelve numbers around the edge of the clock face. The hour hand is placed so that it points at the number on which the checker has been placed. The corresponding time is called “the hour.” For example, if Player A puts a checker on 10, the hour hand is placed so that it points at 10. Player A then says “The hour is 10 o’clock.”
Player B makes a move in two stages: first by placing a checker of a second color on one of the unoccupied numbers, and then by placing a second checker of the same color in such a way that the following is true: The starting hour plus (mod 12) the number of hours corresponding to Player B’s first checker is equal to the time corresponding to Player B’s second checker. The arrow is then made to point at the number on which Player B’s second checker was placed, thus indicating the new hour. Player B then declares the new hour.
Example 1
Suppose Player A begins the game by placing a checker on 10. Then the hour is 10 o’clock. If Player B chooses 4, then his or her first checker is placed on 4, and the second checker is placed on 2 because 10 +12 4 = 2. The hour hand is then moved to 2 o’clock.
Example 2
Suppose Player A chooses 0. If Player B chooses 4, the first checker is placed on 4. In this case, 0 +12 4 = 4, and Player B already has a checker on 4. Therefore, there is no need to place a second checker on 4, and so Player B’s turn ends with the hour being 4 o’clock.
Example 3
Suppose Player A chooses 10 and Player B chooses 0. Then, since 10 o’clock plus 0 hours is 10 o’clock, Player B’s second checker ought to be placed on 10. However, Player A’s checker is already on 10. In this situation, Player B takes Player A’s checker and replaces it with one of his or her own. The hour hand, which was pointing to 10 before Player B’s move began, will not be changed. The hour is still 10 o’clock.
The players continue to alternate turns using rules described in the examples above. If, after completing his or her turn, a player leaves the board so that there are no more unoccupied numbers, then the game is over and the player with the most checkers on the clock wins!