
Note: This story is adapted from our IMACS Math Enrichment Program for talented students in grades 1-8. The solution and analytical process are revealed at the end of this post, so don’t scroll down too far if you want to avoid the spoiler!
Max, The Lost Dog
Sofia, a bright IMACS student, has lost her dog, Max. Luckily, Max was wearing a collar when he was found by another IMACS student, Emily, who loves using her logical reasoning skills to solve mysteries. Tucked into the collar was a piece of paper with clues on where to return Max should he become lost. Follow the clues to help Emily find which house is Max’s so that Sofia can be reunited with her dog … and possibly make a new friend in Emily. (Since both girls take online math classes through eIMACS, they had not met each other yet.)
Clue 1: The number of the house where Max lives is the sum of two numbers, each of which is a power of 2 that is greater than 0 and less than 10. These two numbers that add up to equal Max’s house number can be the same, but they don’t have to be.
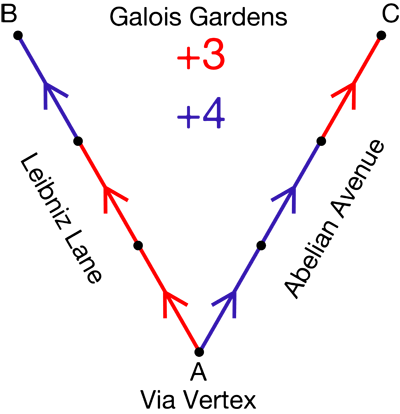
Clue 2: Max lives in Galois Gardens, a neighborhood represented by the following arrow diagram in which each dot represents a house.
The fork to the left is Leibniz Lane, the fork to the right is Abelian Avenue, and the house at the bottom is on Via Vertex. Here is how you interpret the arrows:
• The house number at the end of a red arrow is equal to the house number at the start of that red arrow plus 3.
• The house number at the end of a blue arrow is equal to the house number at the start of that blue arrow plus 4.
Clue 3: The biggest number for any house in the neighborhood is 15.
Clue 4: The number of the house where Max lives is a multiple of 3.
The Analytical Process of Solving the Mystery
Now that you’ve given yourself a chance to work through the problem, let’s go step by step to understand one way we can think about putting the clues together.
Clue 1: What are the powers of 2 that are greater than 0 and less that 10? They are 1=20, 2=21, 4=22, and 8=23. So we need to take one number from the set {1,2,4,8} and a second number from the same set {1,2,4,8} and add them together to come up with the list of possible house numbers. Remember that both numbers can be the same but do not have to be. We’ll leave the arithmetic to you, but we should all arrive at the following possibilities:
Clue 2: Although we don’t yet know any of the house numbers in the arrow diagram of the neighborhood, what can we figure out from the information given? One thing is the location of the house with the smallest number. It has to be the house at the bottom of the picture because the arrows tell us that every time you go from that house along either of the two roads, you add 3 or 4 each time. So you keep getting bigger and bigger house numbers, and they never fall back below the number you started with at the bottom, whatever that number is.
Likewise, is there anything we can say about the largest house number in the neighborhood? Well, it’s probably at the top of the diagram since the house numbers get bigger as you go up the roads. But is it the house on the top left or the one on the top right? Now we need some variables now to help us keep track of these houses.
Let’s call the house number at the bottom “A,” the one on the top left “B,” and the one on the top right “C.”
We know B is bigger than A, and C is bigger than A. Can we say anything about how much bigger B and C are than A? Well, to get from A to B, we add 3 and 3 and 4. That is, we add 10 = 3 + 3 + 4. So A + 10 = B. To get from A to C, we add 4 and 4 and 3. That is, we add 11 = 4 + 4 + 3. So A + 11 = C. We’re starting with at same number, A, and adding 11 to get to C but only 10 to get to B, so C must be bigger than B. Now we know that the house with the biggest number is on the top right.
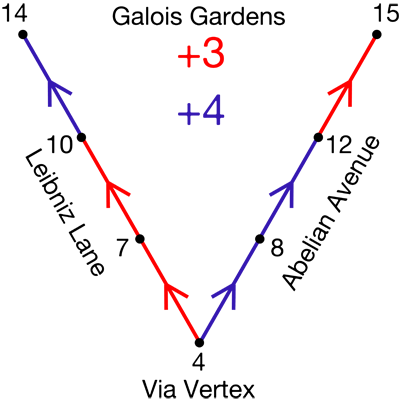
Clue 3: This clue, along with what we figured out from Clue 2, tells us that C = 15. In other words, the address of the house at the top right is 15 Abelian Avenue. With a little arithmetic, we can now determine the rest of the addresses in the neighborhood as follows:
Now that we have all the addresses in the neighborhood, we can go back to our original list of possible house numbers from Clue 1 and cross off the ones that do not show up in the neighborhood. Here’s what our list should look like now:
Clue 4: We’re down to only three possible house numbers—4, 8, and 12. Clue 4 tells us that the house number is a multiple of 3. Which of these possibilities is a multiple of 3? Only 12 is a multiple of 3. Hooray! We figured out where Max lives—12 Abelian Avenue! Sofia will be so happy to have Max back at home, and Emily will be quite pleased with herself for having solved the mystery and done a good deed.










This and many great math posts can be found at the ‘Math Teachers at Play’ blog carnival #48, hosted by Math Is Not A Four Letter Word. Here’s the link >>http://mathfour.com/50word/blog-carnival-for-math-teachers-at-play-number-48-is-here-with-a-fun-twist
[…] Fermat’s Enigma gives us a taste of that cool history book.The clever folks at IMACS shared a fun little logic puzzle: go find Max’s house!Sue visited a second grade class and let them do problems their way – […]