• Information for Parents
• Information for Students
• Information for Educators

A recent study published in the Philosophy of Mathematics Education Journal confirms that teachers’ images of mathematics and their mathematics history knowledge are interlinked. According to the study’s lead author, Danielle Goodwin of the Institute for Mathematics and Computer Science (IMACS), "By and large, the teachers with low history scores in this study were the teachers who exhibited narrow, negative views of mathematics."

Key findings from the study include:

Attitudes Influence Decisions that Affect Students

Why does this matter? Because educators’ views of mathematics affect student learning experiences in a variety of ways, from daily classroom instruction to curriculum selection and development to far-reaching proposals for national math education reform.

Teachers’ images of math are typically based on their own limited experiences as young students, and so teacher education programs should incorporate mathematics history into their curriculum as a way of reshaping attitudes, the study suggests. Doing so would help future teachers develop an appreciation for and understanding of math as a subject that is alive and fundamentally creative. Fostering this viewpoint could help teachers help their students understand that mathematics is a natural place for inventive problem-solving where questioning and investigating are highly valued.

"Teachers who have rule-oriented images of mathematics can weaken student learning by representing mathematics in misleading ways," says Goodwin. Instead of conveying as healthy the struggle of intellectual discovery that naturally takes place in mathematics when new ideas are explored, "struggle" in US K-12 math classrooms has come to mean being "bad at math." This unfortunate association has left generations of Americans hating math and believing in the myth that they are not "math people."

Current teachers and pre-service teachers who want to improve their ability to teach math don’t have to wait for curriculum changes at schools of education. There are wonderful and accessible resources that provide a willing and curious mind with a deeper understanding of mathematics in the context of its rich history.

Recommended Reading and Viewing

If you’re still looking for a holiday gift for your child’s math teacher, perhaps one of the recommended books below would be appreciated. For the visually-inclined,
the videos and movies that follow provide many hours of awe-inspiring and sometimes humorous enlightenment.

The following letter is extracted from the new book, Letters to a Young Math Teacher, by Gerald Rising and Ray Patenaude, which is available from Amazon.com and other sources. Gerry Rising is Distinguished Teaching Professor Emeritus at State University of New York at Buffalo where he co-founded the university’s Gifted Math Program for highly-qualified regional students in grades seven through twelve. Gerry Rising was for many years associated with IMACS activities and is a strong supporter of our work.

Paul Rosenbloom enjoyed an international reputation as a senior mathematician when I joined his Minnemath Project at the University of Minnesota as his assistant director. His Elements of Mathematical Logic remains today a basic resource recognized worldwide to be of historical as well as academic significance.

In our very first conversation he told me that he considered teaching outside the classroom an important aspect of a mathematician’s life and he urged me to develop what he called “a bag of tricks” from which to draw math-related lessons for people of all ages. I would later see him draw from his own collection in a number of settings. He could captivate anyone from nursery school students to scientific colleagues and even senior political figures.

Within a month of that conversation I found myself seated on an airplane flying from Minneapolis to Denver. My seat partners were a bored nine-year-old and her mother. When the mother learned that I was a math teacher, she asked me if I would be willing to “show Marjorie some math.”

Fortunately, I had been reading David Silverman’s book, Your Move, and I had some pennies with me. I played a series of Nim games with Marjorie, finding her an interested opponent and a remarkably quick study.

Nim, for readers unfamiliar with the word, is German for “take” and in this context it applies to games with players taking one or more counters like coins from a collection following a given set of rules.

We started with One Pile Nim. I set out a line of pennies on Marjorie’s tray and explained the rules. We would take turns, at each turn removing one, two or three coins. The winner would be the player who could take the last penny or pennies.* When she quickly determined the strategy for playing, I suggested she challenge her mother. Her eyes lit up as she outplayed her mom.

Now she wanted more. I suggested the misère form of the game: same rules for play but this time the loser forced to take the last coin. Now I had her mother’s full attention as well, but again Marjorie, once she found the winning strategy, could outplay mom.

We went on to play the very simple Two Pile Nim game in which each player takes any number of coins from one of two piles with the winner taking the last coin, but then the less transparent game, Woolworth, which is isomorphic to Two Pile Nim. Woolworth is named for the five-and-ten-cent stores of the 1950s that have been reincarnated as today’s Dollar Stores. On a sheet of paper I drew the following diagram:

I placed nickels and dimes as shown in the figure. One player controls the coins on the left, the other the coins on the right. Players alternate moving either of their coins any number of squares to left or right but without joining or passing the opponent’s coins. The object of the game is to squeeze your opponent so that no moves remain.

By the time I showed Marjorie the connection between Two Pile Nim and Woolworth we were well on our descent into the Denver airport. I was rewarded for our hour together when Marjorie turned to her mother to tell her that she wanted to become a mathematician.

Where do you find lessons like these that require no background and yet are suitable to given age groups? I found mine from two sources: my reading of journals and books about mathematics and my observation of lessons taught by others. Appendix 2 lists a few of the many available book sources.

Now, because it is a good story, I will tell you about my use of a lesson copied from the remarkable teacher, Robert Wirtz.^

Late one school year when I was a math supervisor I was asked by a primary school teacher to demonstrate Stern blocks for her students. Stern blocks are inch cross-section blocks that come in lengths from one to ten inches. Cuisenaire rods are similar but with centimeter dimensions.

I took several sets of Stern blocks to this teacher’s classroom and showed the six-year-olds some of the relationships among them.

The students were excited by the opportunity to mix play with learning, and I was convinced that they were gaining from the lesson. I noticed, however, that their teacher was not happy with the children’s mix of play with learning. Several times she interrupted their activities to tell individuals to be quiet.

It was clear to me that the teacher was convinced that I wasn’t disciplining the children in the way she wished, so I suggested that I return the next day to teach another lesson. Despite her reservations about my conduct of this class, she jumped at the chance to have me return. It was clear that she was happy to pass responsibility for these irrepressible kids off onto anyone she could find.

I had seen Bob teach a lesson to a similar group and the next day followed his model. Before the class I had the teacher gather the students in front of the chalkboard. Saying nothing to them I drew a square on the board and within it marked two star shapes. What I had drawn looked like this:

I pointed to that little tail at the bottom of the figure and turned to the class, holding out the chalk.

Several hands waved and I offered the chalk to one of the wavers. The boy came up and carefully wrote a “2” below the diagram.

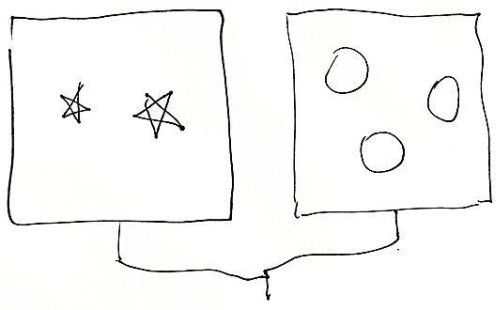
That got us started. I drew similar diagrams with different shapes and the children quickly caught on, competing to write the numbers below the figures. Then I began to complicate the requests by erasing their numbers and connecting two figures like this:

No problem. A volunteer wrote “5” below the boxes.

I continued in this fashion, soon replacing the boxes with numbers but using the same connecting segments. All of the children were eagerly participating, but not one word was said by me or by any of them.

After a half hour of this activity, I finally spoke up, calling the children’s attention to the fact that none of us had spoken until then. And I turned to their teacher to congratulate them on what we had accomplished.

Unfortunately, my lesson proved nothing to this young woman. Her response: “Yes, after you left yesterday I really scolded them for their behavior and you saw the result this morning.”

Even with the best of efforts, you cannot always win.

I have talked about these mathematical extras mostly in terms of their use outside of your classroom, but they can play a role in your classes as well. Here is an example described by Swedish math educator Barbro Grevholm:

Please take the examples I have used only as samples of my own and others’ collections of activities. You may or may not add them to your collection. What is important is that you accumulate such activities that work for you. They will serve you well.

Sources of such activities are all around you. You just have to be alert to them and adapt them creatively.

Many such activities come from your reading. Mathematics and mathematics education journals describe topics and lessons that you can both enjoy and share with others. Of course, you should credit your source when you replicate such a lesson, but every writer I know would be delighted to know that his or her lesson was being duplicated.

The two best journal sources I know for such examples are the Mathematical Association of America’s Math Horizons and the British Mathematical Gazette.

Some non-standard texts are full of such lessons. Authors like Harold Jacobs and Sherman Stein are two who have gathered and present such useful topics. And some authors simply collect such presentations. Among these are Ian Stewart, Ross Honsberger and Howard Eves.

In a class by himself is Martin Gardner whose collections of such topics are unsurpassed. His range is amazing, covering everything from hexaflexagons to fractal music, almost all of them serving a perfect basis for well-planned demonstrations.

Even your daily newspaper can provide activities. Although many people are drawn to the Sudoku puzzles, I much prefer three other popular forms: Kakuro, KenKen and Numbrix. These puzzels are adaptable to students of all ages (I solve one or two each day) and can challenge them all. The simplest appearing is Marilyn vos Savant’s Numbrix. While this puzzle task is appropriate for primary grade students (all it involves is listing the integers from 1 to 81 in order in a 9×9 grid), individual Numbrix puzzles range widely in difficulty.

In addition to their intellectual challenge, there are two things about the Kakuro and KenKen puzzles that I find attractive: (1) they involve basic calculation facts that reinforce the solver’s skills and (2) they appear as free apps on mobile phones and tablets. This availability makes them perfect puzzles to introduce to fellow travelers.

* The strategies for playing these Nim games are included in Appendix 4. I encourage you to play the games before you look at those strategies.

^ Bob Wirtz and his wife adopted a number of children with severe learning problems and they developed math materials to teach them. With Mark Botel, then president of the International Reading Association, he gathered those materials into books for elementary school students. Sadly, they are difficult to find today for they include some very attractive activities.

Abstract reasoning ability entered the national conversation this year as the Common Core State Standards in mathematics were broadly implemented in the United States. In particular, one of the eight Standards for Mathematical Practice is to “reason abstractly and quantitatively.” The so-called STEM subjects — science, technology, engineering and math — are well-known for emphasizing this skill. Given that STEM-related fields are where most high-skilled job growth is predicted, today’s students would do well to develop their ability to think abstractly.

So what is abstract reasoning, and why is it so important? Let’s break it down: To reason is to use logic in piecing together information, usually with the goal of forming an inference or conclusion. Abstract simply means that this process is a thought-based exercise of the mind as opposed to being based in concrete experience. For example, if you know that ice melts at temperatures above 32°F, you can reason abstractly that an ice cube placed on the counter of your room temperature kitchen will melt. You don’t have to take an actual ice cube out of your freezer and observe it for an hour to arrive at this conclusion.

Of the subjects that you could study in order to develop strong abstract reasoning skills, computer science is a natural and practical choice, as well as being a highly creative and exciting area in which to learn and work. The programming aspect of computer science is well-known and is one area where abstract thinking matters a great deal. Programming, after all, is the creation of a set of instructions that a computer can follow to perform a specific task. Such tasks typically involve the manipulation of digital information, decidedly not the kind of stuff you can grab hold of to see how it reacts in the tangible world.

Learning to program well involves developing the ability to think logically and abstractly so that you can anticipate how the computer will react to the instructions you give. Great programmers are actually capable of writing simple code without having to check it with a computer because they have the ability to analyze processes in their minds. If you cannot think abstractly, you may still be able to get your code to “work” with trial-and-error tinkering, but that approach lacks the robustness needed to solve meaningful problems that tend to be more complex.

The rich experience of learning computer science, however, is so much more than coding. When you study computer science, you engage in computational thinking, in which logic, abstraction and creativity come together to help solve intellectually interesting problems. As Professor Jeannette Wing of Carnegie Mellon University argues in her seminal article* on the topic, computational thinking is a skill set from which everyone would benefit no matter their career path.

Why so? Because when you study computer science, your mind learns to grapple with high-level questions such as: How can existing information be used to deduce further information that will help solve the problem? How should a complex system be designed in order to maximize simplicity and usability? How can a complex problem be broken down into smaller pieces that are easier to solve? Can a common approach be devised to efficiently handle similar problems?

If these questions seem like they would be applicable in a wide variety of fields, STEM and non-STEM, it’s because they are. In essence, when you study computer science you learn the valuable skill of thinking abstractly like a computer scientist even if you don’t plan on becoming one.

*Wing, Jeannette M. “Computational Thinking.” Communications of the ACM 49:3 (March 2006) 33-35.

This month, IMACS chats with alumnus Daniel “Danny” Vidaud. Danny started taking IMACS math enrichment classes as an elementary school student and progressed through the introductory computer science class. He went on to earn his B.S.E. in Aerospace Engineering from the University of Michigan. Danny is currently in his third year as an engineer with Boeing.

Tell us about your current position at Boeing. What exactly do you do?

I am an aerodynamics engineer working in technology and product development. In a nut shell, I am part of the team of architects for the external shaping of future commercial jet airplanes. We spend our time sketching up new, outside-the-box ideas and bringing them to life!

What were you like as a kid? What kinds of things interested you?

I was a very intuitive child. Very not normal. Constantly absorbing as much as I could about the world around me. I had a tendency to quickly gain a functional understanding of complex ideas. The downside was that this only applied to topics I found interesting. A repetitive spelling assignment, for example, was as interesting to me as watching paint dry in an empty room with no windows. I needed to actively seek ways to challenge my inspiration or I would inevitably fall into a state of no motivation.

I enjoyed music. The piano, I found, was quite versatile at conveying a variety of musical ideas, but I hated studying it. I couldn’t stand the classical books or the structured process. The musical expression was inspiring; the structured training was not. Instead, I decided that mimicking what I heard on the radio was inspiring enough to practice for hours on end. Free improvisation and jazz composition became the new method of study.

Computer games! Fun! Not so fun when they freeze and get choppy, right? So I decided it would be interesting to develop a theory on what made a computer “fast” or “slow” and subsequently exploit that theory to help others in creating new systems or maintaining their old systems to do what they needed them to do.

Physics and all other things I found interesting went along the same lines of thought. The approach was always the same: Take a complicated problem, gain a general intuitive understanding for how it works, then generate as many permutations or original ideas as possible.

Did you know from a young age that you wanted to be an engineer?

Always. I didn’t always know it was called engineering though. I just knew that I liked asking the “Why not?” question a lot. “Why can’t we do something like this?” Challenging the normal. Being weird. It just seemed like more fun to not do what everyone else was doing.

Given that, rocket science seemed like a viable candidate. No one was doing it, everyone said it was impossible, and it seemed like it might be a good place to start if I wanted to get involved in something really complicated that may have high demand and low supply. So I turned 15, applied with a pre-declared major of Aerospace Engineering to the University of Michigan, a few years later developed a powerful network of friends, and then came to work for Boeing in the heart of its commercial think-tank.

How did your IMACS classes prepare you for college? Your position at Boeing?

The teaching philosophy for computer programming at IMACS is not the classical piano book approach. You will not become an expert at solving any kind of existing, well-defined problem with one specific and popular language. You’ll spend a lot of time not learning the computer language that you will be taught in your first term in college.

Instead, you will gather an understanding of what you might call “computer linguistics”. The ability to communicate an idea through the assembly of conceptual components. The skill of decomposing a multipart task into a simple abstract algorithm. At which point you are then free to cut code in the language that would be most efficient for communicating that idea. IMACS computer science provides you with a different way of thinking, not just an add-on to your résumé about how you can write code in an industry favorite language.

At Boeing, we spend time studying new functional aerodynamic shapes to solve a variety of complex problems while keeping in mind the multidisciplinary nature of every component. With every new idea, you walk through the development process to show that it’s viable, or even patentable. Some of the skills I learned at IMACS allow me to draft up a few quick and dirty scripts in languages I had never coded in before. This allows me to save a significant amount of time repeating similar analytical tasks on multiple candidate solutions or parsing out test data in a useful way. After IMACS, you become more comfortable interacting with the machine and make the most of the computational power you have available at your disposal.

You also have some experience teaching. What do you think the US has to do as a nation to improve math, science and computer science education?

I was a substitute teacher at a high school and subsequently a graduate teaching assistant in a first-year programming course for future engineers at Purdue University.

Successful college students today are very aware of the concept of perceived economic value. Students today are more likely to seek out business-related, social science or history degrees rather than physical science or engineering degrees. It demonstrates a general sentiment that the technical degrees are no longer worth their perceived cost (years and/or intensity of training, accrued financial burden, etc.). Science is not the “cool” thing to do anymore as it once was when scientists were in the limelight of the 60’s. The perceived benefit of being in a technical field was much higher. Marketing happened by default on the news every time a rocket launched at the NASA Kennedy Space Center. Unfortunately, the need for technical degrees is inherently difficult to quantify and isn’t always obvious at a cultural or global economic level anymore.

Today, we’ve come to take for granted the engineering and scientific leaps that have been made in the recent past, such as leaps in wireless data transfer, functional nanotechnology and intuitive human/machine interfaces. Advances in biotechnology research (e.g. replacement organs, spray on skin) have unlocked a new approach for healing the infirm.

Unless the general culture regains an appreciation for scientific exploration by raising the perceived benefits and reducing the perceived cost (as was once shown in the 60’s during the Space Race, or during WWI and WWII in aircraft and military weaponry development, or personal computer development in the late 80’s), we will see a general stagnation in “technological advancement” as it has been traditionally defined.

Traditionally defined innovation and scientific exploration is a high-risk, high-expense endeavor. It will only happen when the global market demands it and demonstrates its true value. When the free market price of oil is allowed to inflate beyond the point of affordability without manipulation, the economy will require immediate and immense creativity in alternative energy and fuel technology. The need for scientists and engineers will be made immediately relevant and the market support will demonstrate the true benefit to all who depend on that which they take for granted.

The traditional ambition within transportation advances, for example, in the past century has repeatedly contained the adjectives “faster, farther, higher”. On the ground we went from conventional rail to high-speed rail (e.g. France’s TGV) to magnetically levitated trains (e.g. Japan’s MLX01). In the air we’ve seen US Air Force-funded demonstrators like the Boeing X-51 flying multiple times the speed of sound over the Pacific Ocean.

It seems the general population is now fairly uninterested in the traditional. We are no longer actively pursuing this long-established goal. In a modern culture that is approaching one of perfect information (made possible, in part, by economically accessible, internet-enabled, naturally intuitive smartphones), we have the ability to make more rational purchasing decisions. Now the market tends to instantly reward those who can make a substitute product for a cheaper price. Engineering and science is being redirected to the practical. For example, after you pick your destination, travel websites will automatically sort by price. The name of the game now isn’t “faster, farther, higher” anymore. The commercial business case is just not there for it.

Social awareness is starting to flow into the demand for science and engineering. Privatized venture philanthropy and private humanitarian and community foundation efforts have created a multi-billion dollar industry in the past 10 years. Modern innovation is making commodities such as digitally-based financial services for the poor or basic health services available to the masses that were previously prohibitively expensive.

Science, Technology, Engineering and Mathematics are here to make the world a better place. How we each define “better” will guide innovation and large private capital into the directions that have highest economical demand and true value. The only thing we can do now is try to show the world what we are capable of accomplishing and what they can do as the culture begins to appreciate, once again, how powerful ideas really are.

It’s that time of year when we think about changes and improvements for the new year. Here are three that IMACS would be delighted to see on every educator’s list:

Teach computer science. The opportunity for American students to learn this increasingly important subject in school is woefully rare. If we want future generations to continue to have a high standard of living, we must prepare them for the jobs of tomorrow. While some of these jobs may not even have been invented yet, we are fairly certain that computational thinking learned through studying computer science will be a highly valued skill needed to succeed at them.

Be a guide, not an answer key. Give students time to puzzle through new concepts and problems and the opportunity to discover answers for themselves. Step in when needed to help avoid frustration. More learning will happen, more knowledge will stick, and more confidence will build for the next challenge.

Give children more unstructured time. This is such a challenging goal in today’s busy and competitive world, but it is well worth the effort. Our culture and history have long emphasized industriousness and productivity (for good reason), but we are now coming to understand that unstructured time is also a highly productive time for our brains. These are the moments when insight and unconstrained creativity lead to new ways of thinking and solving problems. Those are the seeds of progress.

Thank you all for a terrific 2012, and best wishes for a wonderful 2013!

In our previous IMACS blog post, we began our response to Professor Andrew Hacker’s op-ed piece entitled “Is Algebra Necessary?” by taking a critical look at his reasoning in favor of eliminating the requirement for high school algebra. We argued instead that the approach to teaching algebra, and more broadly all of mathematics, should be changed significantly in the US to benefit all students, from those who are struggling to ones who are at maximum achievement under the current limited system. In this week’s post, IMACS discusses key elements that we believe should be part of any effective curriculum in mathematics.

We were pleased to see that Prof. Hacker quoted mathematics professor Peter Braunfeld of the University of Illinois as saying, “Our civilization would collapse without mathematics.” Prof. Braunfeld is not new to the mathematics education debate, having co-authored an article* on the subject with IMACS principal founder, Burt Kaufman, and IMACS curriculum contributor, Professor Vincent Haag, nearly 40 years ago. (Prof. Braunfeld was also a contributor to the IMACS curriculum.) Their article outlined five principles that have and continue to guide IMACS in our curriculum development.

Everything Old is New Again

A 40-year-old article!? How can that be relevant now? Sadly, the circumstances lamented then by the co-authors remain a plague on our US math curriculum to this day. Have you heard anything like the following excerpts lately?

It’s no wonder that students find math dull and tedious. The trivialized curriculum forced upon them has been stripped of all the wonder and beauty of mathematics.

In just the past year, the articles we’ve read suggesting that video tutorials, massive open online courses, and the iPad are going to “revolutionize” education are too many to count. The drive-thru window may have changed how Mickey D’s was served, but the stuff in the paper bag remained of questionable nutritional value for a long time. (Yet even the Golden Arches eventually overhauled its menu!)

Can we say teach to the test? The idea of “industrialized education” came about long before No Child Left Behind. What’s unfortunate is that such an ill-conceived notion wasn’t what was left behind.

Five Guiding Principles of Mathematics Education

So what are the five guiding principles that the co-authors proposed? The excerpts that follow summarize how they believed mathematics should and can be taught to children and how IMACS teaches today:

Exasperated students continue to ask when they are ever going to need high school math in the real world, and who could blame them? Yet you never hear such broad and fervent protest about high school science even though relatively few kids will put that knowledge to work. Why less complaining? Because science curricula, for the most part, still incorporate grand ideas that elicit awe in young minds. Why are parents appalled by cuts in the arts at school? Not because most think their kids will pursue careers in creative fields, but because they understand that the aesthetic experience lifts the human spirit.

Mathematics is brimming with this kind of elemental beauty too. Yet decade after decade, schools use curricula that deprive math students of the good stuff. It’s like feeding the cardboard box instead of the cereal to a kid and saying “See, it says ‘cereal’ right there on the label. How can you say it’s tasteless?” Children have been telling us for too long that we need to change the menu. It’s time we listen.

*”Mathematics Education: A Humanist Viewpoint,” Braunfeld, Peter, Burt A. Kaufman, and Vincent Haag, Education Technology, November 1973.

Editor’s Note: IMACS will soon be rolling out a series of interactive online math courses designed with the five guiding principles discussed above. These courses will allow talented students to complete all of middle and high school mathematics with the exception of calculus before leaving middle school. Check back at www.eimacs.com or like us on Facebook for exciting details to come!

Andrew Hacker, emeritus professor of political science at Queens College, City University of New York, recently wrote an op-ed piece in The New York Times entitled “Is Algebra Necessary?” His opinions caused quite a stir in the ongoing debate over mathematics education in the US. IMACS sees value in some of his ideas, such as teaching quantitative reasoning starting in kindergarten, and we agree that schools should not subject students to the “ordeal” of struggling with algebra. However, IMACS believes that education professionals should focus on changing the way mathematics is taught, not on eliminating the requirement to study algebra.

First, consider the attendant consequences of the author’s proposal, which is to create alternative math courses that “familiarize students with the kinds of numbers that describe and delineate our personal and public lives.” Perhaps the large yet still minority percentage of students who cannot pass traditional algebra would be allowed to satisfy their high school math requirement with these alternative classes. As the author sees it, this would limit “misdirecting precious resources” presumably by redirecting them to the new classes. Does that mean we abandon the majority of students who can pass traditional algebra to the ineffective mores of a failing system (now with even fewer resources) because, hey, at least they’re not struggling? Never mind the fact that neither are they soaring as high as they could and will need to as the influence of technology on their world grows!

Teaching mathematics effectively to all students is the outcome we should be striving toward. Make no mistake—we understand the consequences of the prolonged economic stress on families, school districts, and public higher education. It is natural in such times to direct limited resources to activities most likely to lead to gainful employment. So let’s consider a key element of the author’s argument—that high schools are not even teaching students the math skills they will need in the workplace. He writes:

The author seems to miss the point that the mathematical reasoning skills needed to succeed in the workplace are the same ones needed to succeed in algebra. In both cases, you must be able recognize a problem or challenge, gather information relevant to finding a solution, analyze and synthesize the information to derive a solution, and effectively apply the solution. This takes critical thinking and logical reasoning abilities, and the current pedagogical approach is to try to impart these skills through the process of teaching algebra, almost as a side-effect.

Were the US education system to focus more in elementary school on building these fundamental skills, not only would students find learning high school algebra (and learning in general) easier, they would also be better equipped to succeed in the workplace where problem solvers are highly valued. Furthermore, as learning algebra becomes easier, it becomes less time-consuming, thereby freeing up instructional time to add topics from skill-training to more advanced math as desired. It may sound like an idealistic vision to the millions of people who have come to believe they are “bad at math” when they are more likely the product of bad math curricula, but we have seen this approach work for IMACS students for over 20 years.

Of course considerable training occurs after hiring in STEM fields! The need for accuracy and the complexity of the body of knowledge are so much greater in these fields than in others that are more subjective in nature (e.g., the arts) or that rely more on so-called “soft skills” (e.g., politics). We need only to look to the history of the Space Shuttle to understand the consequences of errors in judgment. On a happier note, consider that the successful entry, descent, and landing of the Mars Science Laboratory was almost 10 years in the making. On-the-job training is necessary in many non-STEM fields from law to portfolio management to journalism to costume design. Why should we expect STEM be any different?

As for the Toyota-sponsored Machine Tool Mathematics class, the course catalog description is “An applied mathematics course designed for machinists which includes instruction and practice in algebraic and trigonometric operations. (2 hour lecture, 2 hour lab).” That doesn’t sound like the math is different from what is taught in high school. Rather it sounds more like the way the math is taught is different. With a hands-on lab, it actually sounds like fun! That is a huge distinction and goes back to our main point that we need to significantly change our approach to how we teach mathematics in the US.

At IMACS, we support the idea of schools using math curricula that accurately incorporate real-world examples that students care about. This approach helps put abstract concepts in context but, more importantly, gets students interested in learning and helps them understand how mathematics shapes our world. Those who appreciate mathematics in its pure and abstract form are pretty special people, but math should and can be accessible to the majority as well. There also need to be more options for visual-spatial learners who may not “get” math concepts when presented on a bland white board. Rather than redirecting limited resources to creating new alternative classes, the focus should be on redesigning the algebra curriculum (as well as those for elementary, middle, and the rest of high school math) to present mathematics for what it truly is, a deep discipline centered around simple but beautiful ideas, rather than a bunch of numbers, funny symbols, and boring algorithms.

“In an online world, colleges have to think hard about how they are going to take communication, which comes over the Web, and turn it into learning, which is a complex social and emotional process.”
-David Brooks, New York Times, May 3, 2012

Over the last 15 years, the advances in our ability to share information broadly and quickly have been nothing short of astounding. More recently, we have started to witness technology’s influence on education. As Peter Haskell, math department chairman at Virginia Tech, said in a recent article, “How could [computers] not change higher education? They’ve changed everything else.”

Computers are indeed changing higher education, as well as elementary and secondary school education. The Danville School District in Indiana announced that it will be piloting an iPad-based program to educate its students by ability level and not by the traditional grade levels. Many see technology as the much-longed-for solution to the 21st century, individualized education that creativity expert, Sir Ken Robinson, espouses.

IMACS has been grouping students by ability level and using technology to provide customized learning experiences for over 20 years, and we’ve learned much in the process. We understand why it is tempting to leverage existing technology, as is, to try to improve education—development costs are little to none, and the solution seems to “fit” the problem “well enough.” However, our experience tells us that a more thoughtful approach yields better outcomes for the students involved.

The popular approach to incorporating technology in education seems to follow the “defense-to-daily life” path. By this we mean that amazing inventions first created for military purposes made their way into daily life after people asked, “How else can this be used?” Examples include digital photography, which came from spy satellites, and the GPS in your car that keeps you from getting lost.

Within the education debate, the analogous line of reasoning is, “We have the technology to distribute and exchange information on a global scale at relatively low cost. Education, in its most basic form, is information. Therefore, technology can be used to widely deliver education. Technology also enables us to track and analyze massive amounts of data. Student performance is essentially data. Therefore, we can use technology to determine when an individual student has learned a topic and is ready to study the next topic.”

One obvious problem is that this approach relies on quantifiable student performance, the kind that computers know how to “think” about. What’s that? None other than answers to multiple choice questions, stand-alone numeric answers, or simplistic word answers. In other words, this approach to individualized learning uses the type of assessment you find with one-size-fits-all standardized testing, which we know does not effectively measure mastery.

Consider the ability to apply learning to novel situations, which is a component of mastery that is generally recognized as the highest of the so-called “learning outcomes.” How could standardized test-like questions ever measure the ability to recognize underlying parallels and to transfer skills acquired in one context to another? Educational technology, while still a net positive, has its limits. It’s hard to imagine a situation in which a computer could reliably grade an essay on “Compare and contrast the lifestyles of the middle class in Manila, Philippines, and Quito, Ecuador.”

For technology to deliver on the promise of turning out well-educated students in greater numbers, methods should be developed for automatic evaluation of student performance that go beyond the multiple-choice paradigm. This includes designing questions that truly test the depth of a student’s understanding, along with systems to assess the quality of answers to such questions. In other words, the technology should be made to fit the curriculum and not the other way around.

Taking this approach means that one does not have to compromise on curriculum development. One has the freedom to create original course material based on what is shown to be effective, knowing that the technology to support it will follow. This is one of our founding principles at IMACS, where we have been researching, developing, and implementing these technologies in our online mathematics and computer science courses since the beginning. The depth of understanding that our students develop leaves us confident that we made the right choice for them.

Education reformers must decide if they will use the building momentum to spread mediocrity all over the place, or if they will push for the bold change necessary to teach students the 21st century skills that they need. Students deserve better than to have the technological tail wag the pedagogical dog.

For innovative courses in gifted math and online computer science, try IMACS! Register for our free aptitude test. Solve weekly IMACS logic puzzles on Facebook.

This week’s post by guest author, Dr. Dora Musielak, includes selected excerpts from her book, Sophie’s Diary: A Mathematical Novel. The story is inspired by French mathematician, Marie-Sophie Germain, the first and only woman in history to make a substantial contribution to the proof of Fermat’s Last Theorem. Little is known of Germain’s adolescence prior to the time she began corresponding with great mathematicians such as Lagrange, Legendre, and Gauss. As Dr. Musielak explains in the MAA Books blog post, this book imagines how Sophie might have learned mathematics on her own during a time when girls and young women were strongly discouraged from such pursuits.

An aerospace engineer scientist by training, Dr. Musielak is currently Researcher and Professor of Physics and Mathematics at the University of Texas Arlington. Dr. Musielak is also a NASA fellow. She is also the author of Kuxan Suum: Path to the Center of the Universe, a book to that combines astronomy and astronautics to promote the exploration of space.

From Sophie’s Diary: A Mathematical Novel

Wednesday — April 1, 1789

How can I divide 35 in a half, a third and a ninth, and get an even number? It seems impossible! Yet I know there must be a way… .

     My name is Sophie. Today is my thirteenth birthday and my parents surprised me with wonderful gifts. My father gave me a lap desk of glossy mahogany wood. It has a compartment to keep paper and pens, and a secret drawer that can only be opened by pressing a hidden tab underneath. When I unlocked it, I found a mathematical riddle and a note from Papa, challenging me to solve it. He gives me a year, but I hope to find the answer sooner than that. Oh, I am so excited!

     My mother gave me a porcelain inkwell, a stack of linen paper, sealing wax, a miniature burner, six bottles of ink in different colors, and a set of quills. These are the best birthday presents ever! I promised my parents to write often to improve my penmanship. Maman says writing neatly and correctly is very important for a refined young lady. This gave me the idea of writing a journal intime, a diary where I can record my innermost thoughts and feelings.

     I love my father. He taught me arithmetic when I was five. I still remember my excitement when Papa taught me the numbers. I used to think that the arithmetic operations were magic tricks to produce new numbers. Just for fun, I spent hours adding numbers to create others. Now I help Papa with the more complicated calculations he needs for his business transactions. He still calls me ma petite élève.

     I have two sisters, Angélique-Ambroise and Marie-Madeleine. Angélique is ten years old, a pretty and vivacious girl who talks incessantly, exactly the opposite of me. Madeleine is almost nineteen years old. She resembles our mother and, like her, she is romantic and sweet. I am not like either of them. My sisters like to dress in beautiful gowns, style their hair, and sing and dance. I don’t like any of that.

     Angélique calls me “peculiar.” She teases me all the time because I like to be alone and would rather read books. I do not care whether my hair is curled, or if my dresses are fashionable. I do not think about these things the way she does. But I am fond of her, just as I am of my mother and Madeleine. I especially love my father with all my heart; mon cher père, he understands me better than anyone.

Monday — January 2, 1792

I begin the new year with more determination and a renewed resolve to study prime numbers. One of my goals is to acquire the necessary mathematical background to prove theorems.

     Prime numbers are exquisite. They are whole pure numbers, and I can manipulate them in myriad ways, as pieces on the chessboard. Not all moves are correct but the right ones make you win. Take, for example, the process to uncover primes from whole numbers. Starting with the realization that any whole number n belongs to one of four different categories:

                   The number is an exact multiple of 4 : n = 4k
       The number is one more than a multiple of 4 : n = 4k + 1
       The number is two more than a multiple of 4 : n = 4k + 2
     The number is three more than a multiple of 4 : n = 4k + 3

It is easy to verify that the first and third categories yield only even numbers greater than 4. For example for any number such as k = 3, 5, 6, and 7, I write: n = 4(3) = 12, and n = 4(6) = 24; or n = 4(5) + 2 = 22, and n = 4(7) + 2 = 30. The resulting numbers clearly are not primes. Thus, I can categorically say that prime numbers cannot be written as n = 4k, or n = 4k + 2. That leaves the other two categories.

     So, a prime number greater than 2 can be written as either n = 4k + 1, or n = 4k + 3. For example, for k = 1 it yields n = 4(1) + 1 = 5, and n = 4(1) + 3 = 7, both are indeed primes. Does this apply for any k? Can I find primes by using this relation? Take another value such as k = 11, so n = 4(11) + 1 = 45, and n = 4(11) + 3 = 47. Are 45 and 47 prime numbers? Well, I know 47 is a prime number, but 45 is not because it is a whole number that can be written as the product of 9 and 5. So, the relation n = 4k + 1 will not produce prime numbers all the time.

     Over a hundred years ago Pierre de Fermat concluded that “odd numbers of the form n = 4k + 3 cannot be written as a sum of two perfect squares.” He asserted simply that n = 4k + 3 ≠ a² + b². For example, for k = 6, n = 4(6) + 3 = 27, and clearly 27 cannot be written as the sum of two perfect squares. I can verify this with any other value of k. But that would not be necessary.

Friday — May 31, 1793

… I discovered a bookshop specialized in mathematics, right on the corner of the quai des Augustins. The shop was empty when we entered, thus allowing me to browse without curious eyes and questioning stares. What I found is indescribable, a treasure of knowledge neatly recorded in the pages of those volumes. New books written by contemporary mathematicians and exquisite translations of ancient manuscripts, all bound in beautiful leather covers and inscribed with golden letters. I was glad that I brought a full purse and purchased Oeuvres d’Archim`ede for 30 francs. It is expensive but I couldn’t let go of it. The book begins with a biographical portrait of Archimedes, then it discussed his memoirs, and it is supplemented with a history of the arithmetic development in Greece.

     I don’t remember the walk back home, as I was anxious to return and read my treasure.

Note: If you enjoyed these select passages, please visit www.sophiesdiary.net to read more extensive excerpts.

Study university-level mathematics with online gifted math courses from IMACS! Register for our free aptitude test. Solve weekly IMACS logic puzzles on Facebook.

In our prior blog post where we discussed the importance of effective teachers for gifted students, we also made the point that such teachers should be armed with higher quality curricula better geared toward bright kids. This week, we delve more deeply into what raises the quality of curricula and renders them more suitable for bringing out the best in talented students.

Fast Forward vs. Delve Deeper

Let’s start with the obvious. Gifted students often understand new information after having it explained to them once. This is in contrast to a typical student who benefits meaningfully from review and reinforcement of new topics. There may be times when gifted children benefit from review, but they generally find repetition unutterably boring. Consequently, bright kids who are subjected to curricula that emphasize review can develop a dislike for school or, in the worst case, of learning.

Advocates of free online resources often point to online technology as a remedy in situations like this because you can skip over the boring parts of a lesson and cover more topics. But who wants to spend time and mental energy searching through a lesson to avoid the repetitive parts? More importantly for talented children, are we really aiming for quantity of topics over quality of learning as a badge of honor for the brightest among us? Gifted students’ time would be better spent gaining a deeper understanding of a subject using material that was specifically designed with their ability level and thirst for knowledge in mind.

Challenge and Failure as Preparation for Success

Online curriculum development for talented students is about more than just going faster and avoiding repetition. It’s about presenting challenging ideas along with the appropriate interactive tools to explore and understand them. It’s about asking questions that require genuine thought to answer rather than just a cursory understanding—or worse, a simple memory—of something. It’s about asking questions in such a way that, in the process of determining the answer, the student’s understanding gets deeper.

Parents and administrators should recognize that accelerating through standard curricula is not the same as studying coursework designed to challenge the gifted mind. Challenging talented students is essential for putting them on a path toward future success. These kids have the potential to solve our most intractable problems and invent products and processes not yet imagined. As anyone who has accomplished even one of these amazing feats will tell you—it’s not a sprint but a marathon fraught with many false turns. This relates to the much-quoted findings by Stanford psychologist Carol Dweck that praising intelligence undermines motivation and performance as compared with praising effort. A child who has not learned to put forth great effort in conquering ability-appropriate challenges or in developing resilience in the aftermath of failure will never reach his or her full potential.

Address Misunderstandings Immediately

For many subjects, including mathematics and computer science, ideas learned at one stage serve as the foundation for learning more complex ideas at later stages. Likewise, a misunderstanding of an earlier concept jeopardizes the understanding of future concepts that build upon it. It can be difficult to dislodge misconceptions that have had some time to settle:

Thus, any praiseworthy online education program should cause students to address a misunderstanding at the moment that they are having it. If you wait until some later time to give a student corrective feedback on their work, the moment of maximum learning has already passed. Remember that we’re talking about young students who are simultaneously learning various new ideas across multiple subjects. When a student is already focused on learning the next topic, it’s less effective to try to bring his or her mind back to an “old” idea.

How an online education program goes about detecting and addressing flaws in student understanding is critical to whether the program is really delivering on its promise to teach in the truest sense of the word. This is not a trivial exercise that can be accomplished by a system that instantly tells you whether a multiple choice selection or one-word answer is correct. Gifted kids can typically regurgitate information from memory or reflect back basic knowledge without much effort. But this doesn’t mean that they understand a topic at a depth commensurate with their ability. Any online curriculum that purports to educate yet relies on several, even many, simply structured questions as a measure of true understanding is short-changing its students, especially the bright ones.

Simply put, talented online students deserve curricula that address their unique intellectual needs along with technological tools designed to fit the particular curriculum and not the other way around. They deserve more than the same material they can get in school with improved presentation and a fast-forward button. Delivering on the promise of educating students online is possible, but it takes much more thought, planning, and investment to do than is widely accepted in the current media coverage and commentary.

Are you a gifted and talented middle or high school student? IMACS offers online courses designed just for you! Take our free aptitude test. Solve weekly IMACS logic puzzles on Facebook.